Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔAKB nội tiếp
AB là đường kính
Do đó: ΔAKB vuông tại K
Xét tứ giác AECK có \(\widehat{AEC}+\widehat{AKC}=90^0+90^0=180^0\)
nên AECK là tứ giác nội tiếp
b: Xét ΔIAB có
BK,IE là các đường cao
BK cắt IE tại C
Do đó: C là trực tâm của ΔIAB
=>AC\(\perp\)IB tại D
Xét tứ giác CEBD có \(\widehat{CEB}+\widehat{CDB}=90^0+90^0=180^0\)
nên CEBD là tứ giác nội tiếp
Xét tứ giác AKCE có \(\widehat{AKC}+\widehat{AEC}=90^0+90^0=180^0\)
nên AKCE là tứ giác nội tiếp
Xét tứ giác IKCD có \(\widehat{IKC}+\widehat{IDC}=90^0+90^0=180^0\)
nên IKCD là tứ giác nội tiếp
Ta có: \(\widehat{DKC}=\widehat{DIC}\)(DIKC nội tiếp)
\(\widehat{EKC}=\widehat{EAC}\)(KAEC nội tiếp)
mà \(\widehat{DIC}=\widehat{EAC}\left(=90^0-\widehat{DBA}\right)\)
nên \(\widehat{DKC}=\widehat{EKC}\)
=>KC là phân giác của góc DKE
Ta có: \(\widehat{KDC}=\widehat{KIC}\)(DIKC là tứ giác nội tiếp)
\(\widehat{EDC}=\widehat{EBC}\)(EBDC nội tiếp)
mà \(\widehat{KIC}=\widehat{EBC}\left(=90^0-\widehat{KAB}\right)\)
nên \(\widehat{KDC}=\widehat{EDC}\)
=>DC là phân giác của góc KDE
Xét ΔKED có
DC,KC là các đường phân giác
Do đó: C là tâm đường tròn nội tiếp ΔKED
=>C cách đều ba cạnh của ΔKED

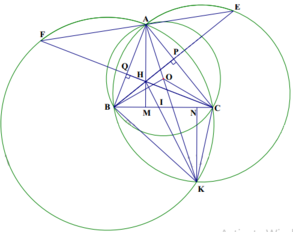
a, Ta có AKB =AEB (vì cùng chắn cung AB của đường tròn ngoại tiếp tam giác AEB)
Mà ABE =AEB (tính chất đối ứng) suy ra AKB= ABE (1)
AKC= AFC (vì cùng chắn cung AC của đường tròn ngoại tiếp tam giác AFC)
ACF= AFC (tính chất đối x
Bài giảng học thử

a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
hay \(sđ\stackrel\frown{AB}=60^0\)

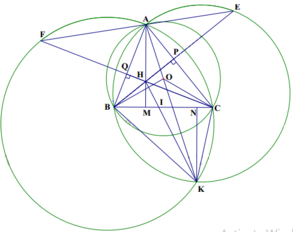
Ta có BOC=120o ;BKC =60o suy ra BOC +BKC =1800 nên tứ giác BOCK nội tiếp đường tròn.
Ta có OB=OC=R suy ra OB= OC=> BKO= CKO hay KO là phân giác góc BKC theo phần (a) KA


