Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi ô chứa hạt thóc thỏa mãn đề bài là ô thứ n ( n ∈ N , n > 1 ) . Khi đó


Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng ( u n ) có u 1 = 7 , d = 5.
Gọi n là số ô trên bàn cờ thì u 1 + u 2 + ⋯ + u n = 25450 = S n .
Ta có 25450 = S n = n u 1 + n n − 1 2 d = 7 n + n 2 − n 2 .5
⇔ 5 n 2 + 9 n − 50900 = 0 ⇔ n = 100
Chọn đáp án B

Chọn D.
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng có u1 = 7; d = 5 .
Gọi n là số ô trên bàn cờ thì u1 + u2 + L + un = 25450 = Sn
Ta có 25450 = Sn = ![]() 5n2 + 9n – 50900 = 0
5n2 + 9n – 50900 = 0
Hay n = 100.

Chọn D
Sau khi chia tiền lần đầu tiên sẽ có 8 trường hợp xảy ra như sau:
| Raashan |
Sylvia |
Ted |
| 1 |
1 |
1 |
| 1 |
1 |
1 |
| 2 |
1 |
0 |
| 2 |
0 |
1 |
| 1 |
2 |
0 |
| 0 |
2 |
1 |
| 1 |
0 |
2 |
| 0 |
1 |
2 |
Các số lần lượt là số tiền của mỗi bạn. Có hai trường hợp cho kết quả (1;1;1) đó là Raashan → Sylvia → Ted Raashan hoặc Raashan Ted Sylvia Raashan.
Với mỗi trường hợp cho kết quả (1;1;1) thì lượt chơi tiếp theo sẽ có 1 4 cơ hội để số tiền mỗi người bằng nhau.
Đối với trường hợp một người có 2$, một người có 1$ và người còn lại không có tiền thì lượt chơi thứ hai sẽ có 4 trường hợp xảy ra. Không mất tính tổng quát ta giả sử Raashan có 2$, Sylvia có 1$ và Ted không có tiền, ta có những cách chuyển tiền như sau:
- Raashan ⇆ Sylvia và Ted không nhận được tiền.
Raashan → Sylvia → Ted.
- Raashan → Ted → Sylvia.
- Sylvia → Raashan → Ted.
Như vậy trong 4 khả năng trên chỉ có một khả năng cho kết quả (1;1;1) chiếm tỉ lệ 1 4
Cứ tiếp tục chơi như vậy đến lượt thứ 2019. Khi đó xác suất mỗi người chơi có 1$ là
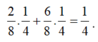

a. Không gian mẫu gồm 20 phần tử được mô tả như sau:
Ω = {(1; 2), (2; 1), (1; 3), (3; 1), (1; 4), (4; 1), (1; 5), (5; 1), (2; 3), (3; 2), (2; 4), (4; 2), (2; 5), (5; 2), (3; 4), (4; 3), (3; 5), (5; 3), (4; 5), (5; 4)}
b. Xác định các biến cố sau:
+ A: "Chữ số sau lớn hơn chữ số trước"
A = {(1; 2), (1; 3), (1; 4), (1; 5), (2; 3), (2; 4), (2; 5), (3; 4), (3; 5), 4; 5)}
+ B: "Chữ số trước gấp đôi chữ số sau"
B = {(2; 1), (4; 2)}
+ C: "Hai chữ số bằng nhau".
C = ∅

Gọi số ngày anh Hải cần phải tiết kiệm là x
Ngày 1 anh hải tiết kiệm được 5000(đồng)
Ngày 2 anh Hải tiết kiệm được 5000+2000(đồng)
Ngày 3 anh Hải tiết kiệm được 5000+2*2000(đồng)
...
Ngày x anh Hải tiết kiệm được 5000+(x-1)*2000(đồng)
Theo đề, ta có:
\(5000+5000+2000+5000+2\cdot2000+...+5000+\left(x-1\right)\cdot2000>=3840000\)
=>\(x\cdot5000+2000\left(1+2+...+x-1\right)>=3840000\)
=>\(5000x+2000\cdot\dfrac{x\left(x-1\right)}{2}>=3840000\)
=>\(5x+\dfrac{2x\left(x-1\right)}{2}>=3840\)
=>\(5x+x^2-x>=3840\)
=>\(x^2+4x-3840>=0\)
=>(x-60)(x+64)>=0
=>\(\left[{}\begin{matrix}x>=60\\x< =-64\left(loại\right)\end{matrix}\right.\)
Vậy; anh hải cần để dành 60 ngày để đủ số tiền mua đôi giày
Do mỗi lần sau tiền đặt gấp đôi lần tiền đặt cọc trước đó
Nên ta có cấp số nhân : \(u_1=20000,q=2\) ( Với \(u_1\) tính bằng đồng )
Số tiền người đó thua là tổng của 9 số hạng đầu tiên cấp số nhân
\(S_9=\dfrac{u_1.\left(1-q^9\right)}{1-q}=\dfrac{20000\left(1-2^9\right)}{1-2}=10220000\) (đồng)
Số tiền người đó thắng là số hạng thứ 10 của cấp số nhân
\(u_{10}=u_1.q^{10-1}=20000.2^9=10240000\) (đồng)
Vì : \(10240000>10220000\) nên du khách đã thắng trong vụ cược này
Số tiền thắng : \(10240000-10220000=20000\) (đồng)
Số tiền du khác đặt trong mỗi lần là một cấp số nhân có �1=20000u1=20000 và công bội �=2.q=2.
Du khách thua trong 99 lần đầu tiên nên tổng số tiền thua là: �9=�1+�2+...+�9=�1(1−�9)1−�=10220000S9=u1+u2+...+u9=1−pu1(1−p9)=10220000.
Số tiền mà du khách thắng trong lần thứ 1010 là �10=�1.�9=10240000u10=u1.p9=10240000.
Ta có �10−�9=20000>0u10−S9=20000>0 nên du khách thắng 2020 000000.