
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mk nghĩ là nếu nhún thì sẽ có đà nhảy lên nhưng mà k nhún vẫn có thể nhảy lên mà =)) haha
ht
ht
ht
ht
ht
TL:
Nếu không nhún chân khi nhảy lên thì sẽ không có lực để có thể nhảy lên
Mik ko chắc nha
@@@@@@
HT

O x > A B
Chọn trục toạ độ như hình vẽ trên, gốc toạ độ trùng với A. Chọn mốc thời gian lúc 8h.
Phương trình chuyển động biến đổi đều có dạng: \(x=x_0+v_0.t+\dfrac{1}{2}a.t^2\)
Xe từ A có: \(x_0=0;v_0=10;a=-0,2\)
\(\Rightarrow x_A=10.t-0,1.t^2 (m)\)
Xe từ B có: \(x_0=560;v_0=0;a=-0,4\)
\(\Rightarrow x_B=560-0,2.t^2 (m)\)
Em gõ câu hỏi gửi lên nhé. Quy định của hoc24 là không gửi câu hỏi dạng hình ảnh.


bài 26: gọi quãng đường đi là S
=|> thời gian đi với v1: t1=S/12
thòi gia đi quãng đường với v2 là :t2=S/15
theo đề ta có pt: t1=t2+1
<=>\(\frac{S}{12}=\frac{S}{15}+1\)
<=> \(\frac{S}{60}=1\)
=> S=60km


2.4
gia tốc của hệ
\(\overrightarrow{a}=\dfrac{\overrightarrow{P_a}+\overrightarrow{P_b}+\overrightarrow{Q_a}+\overrightarrow{Q_b}+\overrightarrow{F_{msa}}+\overrightarrow{F_{msb}}}{m_a+m_b}\)
chiếu trên trục Ox có phương sogn song với mặt phẳng nghiêng chiều dương cùng chiều chuyển động
a=\(\dfrac{sin\alpha.P_a+sin\alpha.P_b-F_{msa}-F_{msb}}{m_1+m_2}\)
\(\Leftrightarrow a=sin\alpha.m_a.g+sin\alpha.m_b.g-k_a.cos\alpha m_a.g\)\(-k_b.cos\alpha.m_b.g\))/(m1+m2)
\(\Leftrightarrow\)\(a=\left(\dfrac{sin\alpha\left(m_a+m_b\right).g-cos\alpha.g\left(k_a.m_a+k_b.m_b\right)}{m_a+m_b}\right)\)
xét riêng vật A: các lực tác dụng vào A, trọng lực Pa, phản lực Qa, lực ma sát Fmsa, lực do vật B tác dụng vào khi trượt xuống F cùng chiều chuyển động
\(\overrightarrow{F}+\overrightarrow{Q_a}+\overrightarrow{P_a}+\overrightarrow{F_{msa}}=m.\overrightarrow{a}\)
chiếu lên chiều dương cùng chiều chuyển động phương sogn song với mặt phẳng
F=\(\dfrac{g.cos\alpha.\left(k_a-k_b\right).m_b.m_a}{m_a+m_b}\)
b) để hai vật trượt xuống a\(\ge\)0
\(\Leftrightarrow\)..........
2.4
b)
\(a\ge0\)
\(\Leftrightarrow\)sin\(\alpha.\left(m_a+m_b\right).g\ge g.cos\alpha.\left(k_a.m_a+k_b.m_b\right)\)
\(\Rightarrow tan\alpha\ge\dfrac{\left(k_a.m_a+k_b.m_b\right)}{\left(m_a+m_b\right)}\Rightarrow\alpha\ge....\)

a)
- a phụ thuộc vào F (m + M = 0, 5kg)
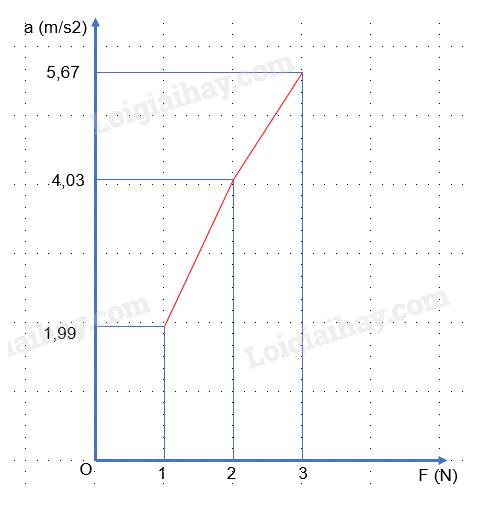
Ta có:
+ Khi F = 1 N, a = 1,99 m/s2 thì \(\frac{F}{a} = \frac{1}{{1,99}} \approx 0,5\)
+ Khi F = 2 N, a = 4,03 m/s2 thì \(\frac{F}{a} = \frac{2}{{4,03}} \approx 0,5\)
+ Khi F = 3 N, a = 5,67 m/s2 thì \(\frac{F}{a} = \frac{3}{{5,67}} \approx 0,5\)
=> Tỉ số \(\frac{F}{a}\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào F là một đường thẳng
- a phụ thuộc vào \(\frac{1}{{m + M}}\) (ứng với F = 1 N)
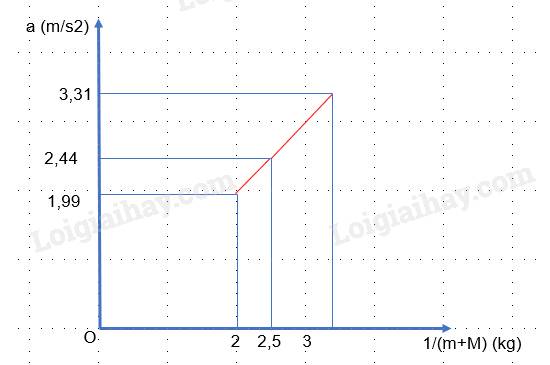
Ta có:
+ Khi a = 3,31 m/s2 , \(\frac{1}{{M + m}} = \frac{{10}}{3}\) thì a. (M + m) = 1
+ Khi a = 2,44 m/s2 , \(\frac{1}{{M + m}} = 2,5\) thì a. (M + m) = 1
+ Khi a = 1,99 m/s2 , \(\frac{1}{{M + m}} = 2\) thì a. (M + m) = 1
=> Tỉ số \(\frac{a}{{\frac{1}{{M + m}}}} = a.(M + m)\) không đổi nên đồ thị sự phụ thuộc của gia tốc a vào \(\frac{1}{{M + m}}\) là một đường thẳng.
b) Ta có:
+ Khi (m + M) không đổi, F tăng thì a cũng tăng => Gia tốc a tỉ lệ thuận với lực F
+ Khi F không đổi, a giảm thì (m+M) tăng => Gia tốc a tỉ lệ nghịch với khối lượng
=> Kết luận: Gia tốc tỉ lệ thuận với lực tác dụng và tỉ lệ nghịch với khối lượng.




 m.n giúp mk với..đang cần gấp ak
m.n giúp mk với..đang cần gấp ak




 G
G


a) thời gian từ nhà đến siêu thị lần 1 : 7 05 - 7 00= 5 p
đổi 5p =300 giây(s)
tốc độ trung bình 50:300 = 1/6 m/s
b) tốc độ trung bình từ siêu thị về nhà 50:360 =5/36 m/s
thời gian từ nhà đến trường: 7 30 - 7 12 = 18 p
đổi 18p = 1080 s
đổi 1km = 100
vận tốc từ nhà đến trường sau 7 12 là 1000:1080=25/17 m/s
vận tốc rung bình từ nhà đến trường từ 7 00 là :
(1/6 + 5/36 + 25/17): 3= 1087/1836 m/s
bonus : vận tốc tb = tốc độ trung bình
ghi 2 lần làm gì bạn:))