Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Giá trị trung bình \(\overline X = \dfrac{{3,5 + 9,2 + 9,2 + 9,5 + 10,5}}{5}\) \( = 8,38\)
Nên dùng trung vị để thể hiện mức lương khởi điểm của sinh viên tốt nghiệp từ trường đại học này vì có giá trị bất thường là 3,5 (lệch hẳn so với giá trị trung bình)
b) Nên dùng khoảng tứ phân vị để đo độ phân tán vì độ phân tán không bị ảnh hướng bởi giá trị bất thường.

'''''''''''''F'F'S'JURSMJHYT,JTHDNHTDNMYHJFGJHTMJHTMJYT

Sắp xếp lại:
5 | 31 | 37 | 43 | 43 | 57 | 62 | 63 | 78 | 80 | 91 |
Khoảng biến thiên R=91-5=86
Ta có: \({Q_2} = 57,{Q_1} = 37,{Q_3} = 78\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 78 - 37 = 41\)
Số trung bình \(\overline X \approx 53,64\)
Ta có bảng sau:
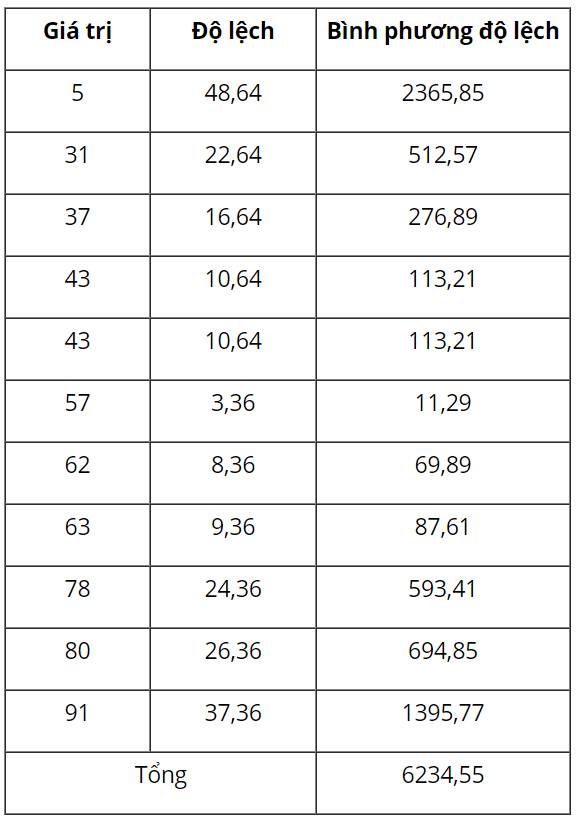
Độ lệch chuẩn là 79
Môn Tiếng Anh:
Sắp xếp lại:
37 | 41 | 49 | 55 | 57 | 62 | 64 | 65 | 65 | 70 | 73 |
Khoảng biến thiên R=73-37=36
Ta có: \({Q_2} = 62,{Q_1} = 49,{Q_3} = 65\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 65 - 49 = 16\)
Số trung bình \(\overline X = 58\)
Ta có bảng sau:
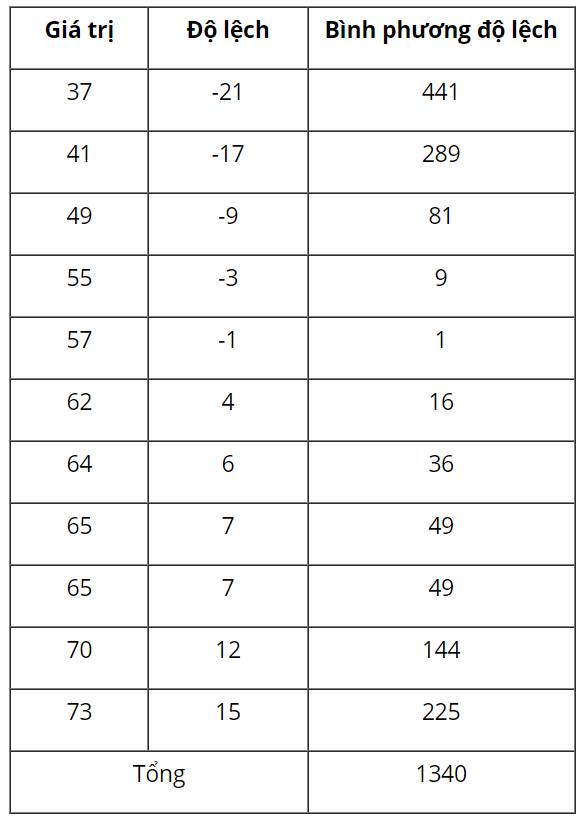
Độ lệch chuẩn là 36,6
Từ các số trên ta thấy mức độ học tập môn Tiếng Anh không đều bằng môn Toán.Độ lệch chuẩn là 36,6

a) Sắp xếp theo thứ tự không giảm:
0 0 0 0 0 0 0 4 6 10
Số trung bình: \(\overline X = \dfrac{{0.7 + 4 + 6 + 10}}{{10}} = 2\)
Trung vị: \({Q_2} = 0\)
+ Mốt: 0
Tứ phân vị:
+ Nửa bên trái của \({Q_2}\):
0 0 0 0 0
=>\({Q_1} = 0\)
+ Nửa bên phải của \({Q_2}\):
0 0 4 6 10
=>\({Q_3} = 4\)
b) Tứ phân vị thứ nhất và trung vị trùng nhau vì mật độ của mẫu số liệu tập trung hết ở nửa trái của trung vị, mẫu số liệu bên trái có số liệu bằng 0 hết.

a) Nhà máy A:
+) Số trung bình: \(\overline x = \frac{{4 + 5 + 5 + 47 + 5 + 6 + 4 + 4}}{8} = 10\)
+) Mốt: \({M_o} = 4,{M_o} = 5\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 4; 4; 4; 5; 5; 5; 6; 47.
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu: 4; 4; 4; 5. Do đó \({Q_1} = 4\)
\({Q_3}\) là trung vị của nửa số liệu: 5; 5; 6; 47. Do đó \({Q_3} = 5,5\)
+) Phương sai \({S^2} = \frac{1}{8}\left( {{4^2} + {5^2} + ... + {4^2}} \right) - {10^2} = 196\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 14\)
Nhà máy B:
+) Số trung bình: \(\overline x = \frac{{2 + 9 + 9 + 8 + 10 + 9 + 9 + 11 + 9}}{9} = 8,4\)
+) Mốt: \({M_o} = 9\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 8; 9; 9; 9; 9; 9; 10; 11
\({Q_2} = {M_e} = 9\)
\({Q_1}\) là trung vị của nửa số liệu: 2; 8; 9; 9. Do đó \({Q_1} = 8,5\)
\({Q_3}\) là trung vị của nửa số liệu: 9; 9; 10; 11. Do đó \({Q_3} = 9,5\)
+) Phương sai \({S^2} = \frac{1}{9}\left( {{2^2} + {9^2} + ... + {9^2}} \right) - 8,{4^2} = 6,55\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 2,56\)
b)
Nhà máy A có: \({\Delta _Q} = 1,5\)
Vậy giá trị ngoại lệ \(x > 5,5 + 1,5.1,5 = 7,75\) hoặc \(x < 4 - 1,5.1,5 = 1,75\) là 47.
Nhà máy B có: \({\Delta _Q} = 1\)
Vậy giá trị ngoại lệ \(x > 9,5 + 1,5.1 = 11\) hoặc \(x < 8,5 - 1,5.1 = 7\) là 2.
Ta so sánh trung vị: \(9 > 5\), do dó công nhân nhà máy B có mức lương cao hơn.
Chú ý
Ta không so sánh số trung bình vì có giá trị 47 quá lớn so với các giá trị còn lại.

Sắp xếp theo thứ tự không giảm.
2,593 2,977 3,155 3,270 3,387 3,412 3,813 3,920 4,042 4,236
Khoảng biến thiên \(R = 4,236 - 2,593 = 1,643\)
Vì n=10 nên ta có:
\({Q_1} = 3,155\); \({Q_3} = 3,920\)
Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 3,920 - 3,155\)\( = 0,765\)
\(\overline x \approx 3,481\)
Ta có:
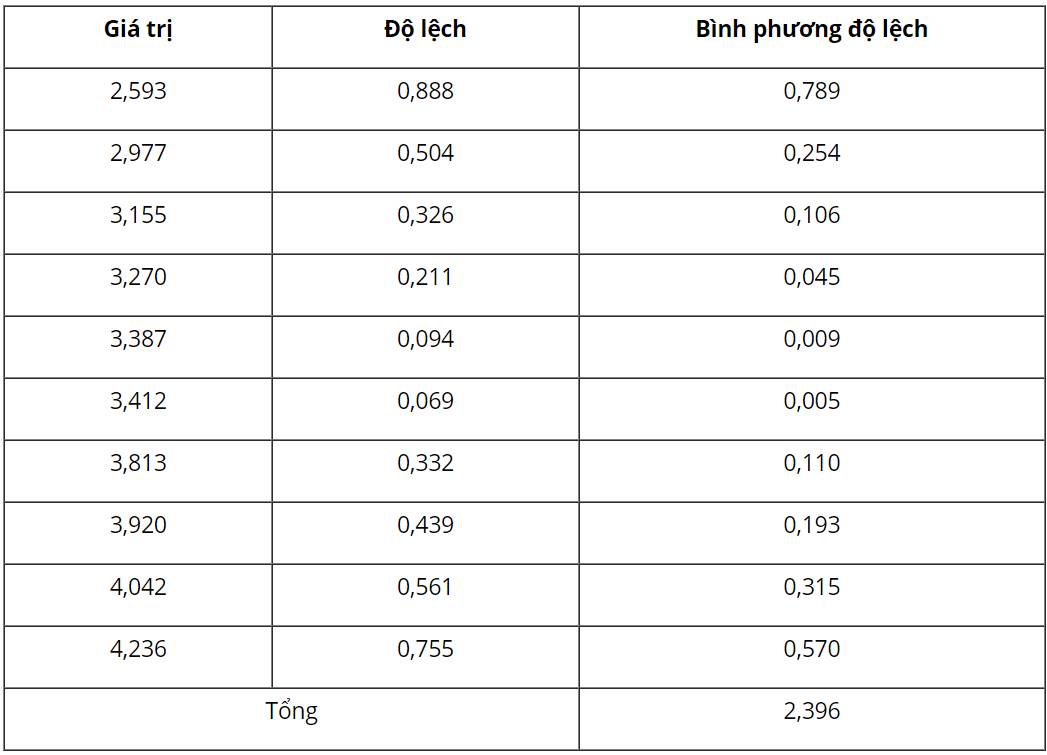
Độ lệch chuẩn: \(s = \sqrt {0,2396} \approx 0,489\)Phương sai là: \({s_2} = \frac{{2,396}}{{10}} = 0,2396\)

- Mức lương bình quân của các cán bộ và nhân viên công ty là số trung bình của bảng lương:
- Số trung bình:
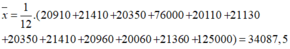
Sắp xếp các số liệu theo dãy tăng dần:
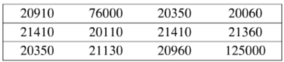
20060; 20110; 20350; 20350; 20910; 20960; 21130; 21360; 21410; 21410; 76000; 125000.
Số trung vị: Me = (20960 + 21130)/2 = 21045.
Ý nghĩa: Số trung vị đại diện cho mức lương trung bình của nhân viên (vì trong trường hợp này chênh lệch giữa các số liệu quá lớn nên không thể lấy mức lương bình quân làm giá trị đại diện).

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
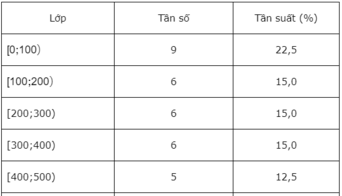
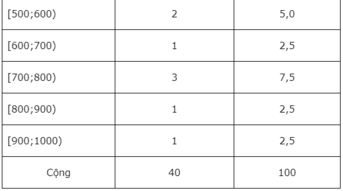
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
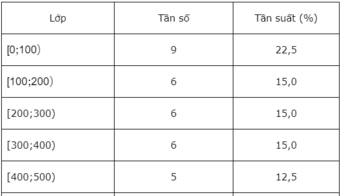
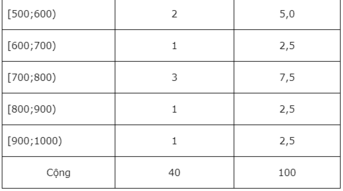
b) b) Cộng các tần suất của bốn lớp [300;400), [400;500), [500;600), [600;700) ta được 15+ 12,5+ 5+ 2,5 = 35. Đáp án là B.



a) Giá trị trung bình ¯¯¯¯¯X=(3,5+9,2+9,2+9,5+10,5):5
X¯=3,5+9,2+9,2+9,5+10,55
= 8,38 ( triệu)
Dùng trung vị để thể hiện mức lương khởi điểm của sinh viên tốt nghiệp từ trường đại học này vì có giá trị bất thường là 3,5 (lệch hẳn so với giá trị trung bình)
b) Chúng ta nên dùng khoảng tứ phân vị để đo độ phân tán vì độ phân tán không bị ảnh hướng bởi giá trị bất thường.
a) Giá trị trung bình ¯¯¯¯¯X=(3,5+9,2+9,2+9,5+10,5):5
X¯=3,5+9,2+9,2+9,5+10,55
= 8,38 ( triệu)
Dùng trung vị để thể hiện mức lương khởi điểm của sinh viên tốt nghiệp từ trường đại học này vì có giá trị bất thường là 3,5 (lệch hẳn so với giá trị trung bình)
b) Chúng ta nên dùng khoảng tứ phân vị để đo độ phân tán vì độ phân tán không bị ảnh hướng bởi giá trị bất thường.