MP
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 9 2021
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng nằm trên một đường tròn
b: Tâm là trung điểm của AC
24 tháng 9 2021
a: Xét tứ giác ABCD có \(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
b: Tâm là trung điểm của AC
Bán kính là \(\dfrac{a\sqrt{2}}{2}\)
20 tháng 9 2021
a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
\(R=\dfrac{AC}{2}\)
12 tháng 9 2021
Vì \(AD//BC\) nên \(\widehat{A}+\widehat{B}=180\left(trong.cùng.phía\right)\)
\(\Rightarrow ABCD\) nt đường tròn
Vì \(OA=OC=R\) nên \(O\in\) đường trung trực AC
Vì \(AB=BC=\dfrac{1}{2}AD\) nên \(B\in\) đường trung trực AC
\(\Rightarrow OB\) là đường trung trực của \(AC\)
Vậy \(OB\perp AC\)
12 tháng 9 2021
Xét tứ giác ABCD có
\(\widehat{A}+\widehat{D}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
CT
24 tháng 9 2021
a: Xét tứ giác ABCD có
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc một đường tròn
b: Tâm là trung điểm của AC
CM
18 tháng 8 2019
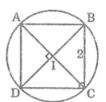
Gọi I là giao điểm của hai đường chéo AC và BD.
Ta có: IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.