K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SN
1
MM
1
27 tháng 12 2021
\(x^2-2x+3=\left(x^2-2x+1\right)+2=\left(x-1\right)^2+2\ge2\forall x\in R\)
OY
21 tháng 10 2021
a) \(2x^2+2x+1=0\)
\(\Rightarrow2x^2+2x=-1\)
\(\Rightarrow2x\left(x+1\right)=-1\)
⇒ Pt vô nghiệm
21 tháng 10 2021
a: \(2x^2+2x+1=0\)
\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)
Vì Δ<0 nên phương trình vô nghiệm
NT
1
26 tháng 7 2023
a: x>2
y>2
=>x+y>2+2=4
x>y>2
=>xy>2^2=4
b: x^2-xy=x(x-y)
x-y>0; x>0
=>x(x-y)>0
=>x^2-xy>0
y>2
=>y-2>0
=>y(y-2)>0
=>y^2-2y>0
x>y và y>2
=>y>0 và x-y>0
=>y(x-y)>0
=>xy-y^2>0
TT
1
2 tháng 10 2021
\(-y^2+2y-4=-\left(y^2-2y+1\right)-3=-\left(y-1\right)^2-3\le-3< 0\forall y\)
PT
1
16 tháng 5 2017
Ta có: \(x^2+y^2+6>4x+2y\)
\(\Leftrightarrow x^2+y^2+6-4x-2y>0\)
\(\Leftrightarrow x^2-4x+4+y^2-2y+1+1>0\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y-1\right)^2+1>0\)(*)
mà \(\left(x-2\right)^2\ge0;\left(y-1\right)^2\ge0;1>0\)
=> (*) đúng
=> \(x^2+y^2+6>4x+2y\)
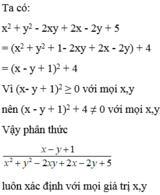
\(x^2+y^2+x-2y+100=\left(x^2+2.\frac{1}{2}.x+\frac{1}{4}\right)+\left(y^2-2y+1\right)+98\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\left(y-1\right)^2+98\frac{3}{4}\ge98\frac{3}{4}\)