SV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 5 2021
Đoán đề: \(\dfrac{x^2-1}{\left(x+1\right)\left(x^2-x-6\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-3\right)\left(x+2\right)}\ge0\)
Xét x-1=0 <=> x=1
x+1=0 <=> x=-1
x-3=0 <=> x=3
x+2=0 <=>x=-2
Bảng xét dấu:
Để VT \(\ge0\) <=> x\(\in\left(-2;-1\right)\cup\left(3;+\infty\right)\cup\left\{1\right\}\)
TA
27 tháng 5 2021
TH1: `m=0 `
`2x>0 <=> x>0`
`=>` Không thỏa mãn.
TH2: `m>0`
Bất PT có tập nghiệm là `RR <=> \Delta'<0`
`<=> (m-1)^2-m.4m<0`
`<=> m<-1 ; 1/3 <m`
Vậy `m in (0;+∞)` thỏa mãn.
27 tháng 5 2021
TH1 là m=0 thì TH2 là \(m\ne0\)
Bpt có tập nghiệm là R <=> \(\left\{{}\begin{matrix}a>0\\\Delta'< 0\end{matrix}\right.\)
Đáp án: m\(\in\left(\dfrac{1}{3};+\infty\right)\)
13 tháng 9 2021
P(x) = (x - a) (x- a - 2015). g(x) => P(x) chẵn với mọi x
Q(x) = (x - 2014) h(x) + 2016 -> Q(P(x)) = (P(x) - 2014 ).H(P(x)) + 2016 chia hết cho 2 nên Q(P(x) = 1 sẽ không thể có nghiêm nguyên
K
0
9 tháng 7 2021
Điều kiện xác định x∈Rx∈R.
Đặt t=√x2+1 (t≥1t≥1)
Phương trình trở thành t2−1−4t−m+1=0
⇔t2−4t=m
⇔t2−4t=m. (1)
Để phương trình có 44 nghiệm phân biệt thì phương trình (1) có hai nghiệm phân biệt lớn hơn 11.
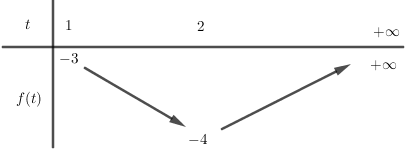
Xét hàm số f(t)=t2−4t có đồ thị là parabol có hoành độ đỉnh x=2∈(1;+∞) nên ta có bảng biến thiên:
Dựa BBT ta thấy để (1) có hai nghiệm phân biệt lớn hơn 11 thì −4<m<−3
Vậy không có giá trị nguyên của mm thỏa mãn yêu cầu bài toán.
NH
Có bao nhiêu giá trị nguyên của tham số m để phương trình x^2 -2|x| +1-m = 0 có 4 nghiệm phân biệt ?
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2021
Đặt \(\left|x\right|=t\ge0\)
\(\Rightarrow t^2-2t+1-m=0\) (1)
Phương trình (1) là bậc 2 nên có đối đa 2 nghiệm t
Với mỗi giá trị \(t>0\) cho 2 nghiệm x tương ứng nên pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=1-\left(1-m\right)>0\\t_1+t_2=2>0\\t_1t_2=1-m>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< 1\end{matrix}\right.\) \(\Leftrightarrow0< m< 1\)
15