K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VD
2
1 tháng 5 2023
`P(x)=2x^3+x^2+5-3x+3x^2-2x^3-4x^2+1`
`= (2x^3-2x^3)+(x^2+3x^2-4x^2)-3x+(5+1)`
`= -3x+6`
Thay `x=0`
`P(0)=-3*0+6=6`
Thay `x=-1`
`P(-1)=(-3)*(-1)+6=3+6=9`
Thay `x=1/3`
`P(1/3)=(-3)*1/3+6=-1+6=5`
VD
2
H
3 tháng 5 2023
\(a,2x^3.\left(-3x^2+5\right)=2x^3.\left(-3x^2\right)+2x^3.5=-6x^{3+2}+10x^3\\ =-6x^5+10x^3\\ b,-2x^4+5x^4=\left(-2+5\right)x^4=3x^4\)
VD
2
H
3 tháng 5 2023
a,
\(C\left(x\right)=A\left(x\right)+B\left(x\right)=x-2x^3+3-4+2x^2+x^3-2x\\ =\left(-2x^3+x^3\right)+\left(2x^2\right)+\left(x-2x\right)+\left(3-4\right)\\ =-x^3+2x^2-x-1\)
b, Thay \(x=2\) vào \(C\left(x\right)\)
\(\Rightarrow-\left(2\right)^3+2.2^2-2-1=-3\ne0\)
\(\Rightarrow x=2\) không là nghiệm của đa thức
VD
2
11 tháng 5 2023
\(A=x^5-4x^4+x^3+x^4-4x^3+x^2+5x^2-20x+5+2023\)
=2023
VD
2
1 tháng 5 2023
`7,`
`B(x)=2x^4-3x^3+x-4x^2+5`
Bậc của đa thức: `4`
Các hệ số của đa thức: `2 ; -3 ; 1 ; -4 ; 5`
`8,`
`a,`
`P(x)=7x^3+3x^4-x^2+5x^2-6x^3-2x^4+2017-x^3`
`= (3x^4-2x^4)+(7x^3-6x^3-x^3) +(-x^2+5x^2)+2017`
`= x^4+4x^2+2017`
Bậc của đa thức: `4`
`b,`
Các hệ số của đa thức: `1 ; 4 ; 2017`
Hệ số cao nhất: `1`
Hệ số tự do: `2017`
VD
2
1 tháng 5 2023
`9,`
`a.`
`P(x)=2+7x^5-4x^3+3x^2-2x-x^3+6x^5`
`= (7x^5+6x^5)+(-4x^3-x^3)+3x^2-2x+2`
`= 13x^5-5x^3+3x^2-2x+2`
`b,` Các hệ số của đa thức: `13; -5; 3; -2; 2`
`c,`
Bậc của đa thức: `5`
Hệ số cao nhất: `13`
Hệ số tự do: `2`
VD
3
1 tháng 5 2023
`12,`
Vì `\Delta ABC = \Delta DEG`
`->`\(\text{AB = DE, BC = EG, AC = DG}\)
`->`\(\text{DE = 5 dm, EG = 7 dm, DG = 8,5 dm}\)
P của `\Delta DEG` là:
`5+7+8,5=20,5 (dm)`
Xét các đáp án trên `-> C.`
VD
2
12 tháng 5 2023
2:
a: P(x)+Q(x)
=2x^3-3x^2+x+x^3-x^2+2x+1
=3x^3-4x^2+3x+1
b: P(x)-Q(x)
=2x^3-3x^2+x-x^3+x^2-2x-1
=x^3-2x^2-x-1
VD
2
12 tháng 5 2023
3:
a: P(x)+Q(x)
=2x^4+2x^3-3x^2+x-6+x^4-x^3-x^2+2x+1
=3x^4+x^3-4x^2+3x-5
b: Q(x)-P(x)
=x^4-x^3-x^2+2x+1-2x^4-2x^3+3x^2-x-6
=-x^4-3x^3+2x^2+x-5
VD
2
12 tháng 5 2023
5:
a: P(x)=x^4+3x^3+x^2+2x+2
Q(x)=x^4+x^3+2x^2+2x+1
b: P(x)+Q(x)=2x^4+4x^3+3x^2+4x+3
P(x)-Q(x)=2x^3-x^2+1
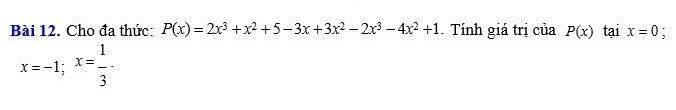
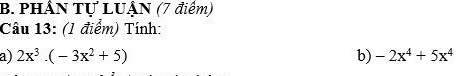
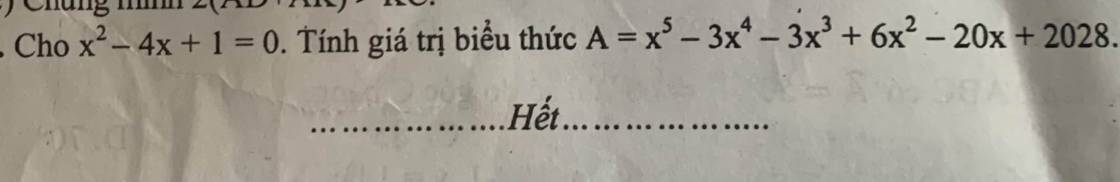
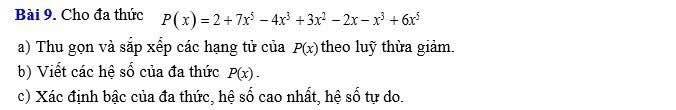
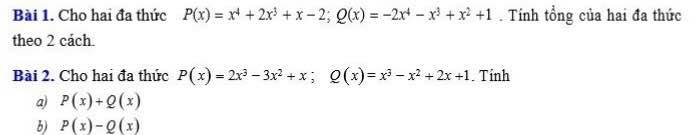
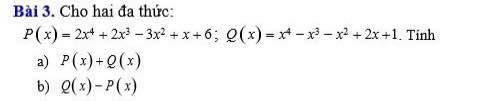
Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x^2+2y^2}{300}=\frac{x^2-2y^2}{294}=\frac{x^2+2y^2+x^2-2y^2}{300+294}=\frac{2x^2}{594}=\frac{x^2}{297}=\frac{x^2+2y^2-x^2+2y^2}{300-294}\)
\(=\frac{4y^2}{6}=\frac{y^2}{1,5}\)
\(\Rightarrow\frac{x^2}{297}=\frac{y^2}{1,5}\)
\(\Rightarrow\frac{x^2}{594}=\frac{y^2}{3}\)
\(\Rightarrow\frac{x^2}{y^2}=\frac{594}{3}=198\)
Vậy \(\frac{x^2}{y^2}=198\)
cảm ơn anh nhiều!!