HA
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
2
25 tháng 11 2021
\(4\times\left(x+5\right)^3-7=101\)
\(\Rightarrow4\times\left(x+5\right)^3=101+7\)
\(\Rightarrow4\times\left(x+5\right)^3=108\)
\(\Rightarrow\left(x+5\right)^3=108\div4\)
\(\Rightarrow\left(x+5\right)^3=27\)
\(\Rightarrow\left(x+5\right)^3=3^3\)
\(\Rightarrow x+5=3\)
\(\Rightarrow x=3-5\)
\(\Rightarrow x=-2\)
Keuka
25 tháng 11 2021
4(x+5)3-7=101
4(x+5)3=101+7
4(x+5)3=108
(x+5)3=108:4
(x+5)3=27
(x+5)3=33
=> x+5=3
x=3-5
x=-2
Vậy x=-2
HM
4
15 tháng 4 2020
\(x\left(y-1\right)=-9\)
Ta có : -9 = 1 . ( -9 )
= -1 . 9
= 3 . ( -3 )
Ta có bảng sau
| x | 1 | -1 | 9 | -9 | 3 | -3 |
| y-1 | -9 | 9 | -1 | 1 | -3 | 3 |
| y | -8 | 10 | 0 | 2 | -2 | 4 |
Vậy các cặp số nguyên (x;y) thỏa mãn là :
(1; -8) ; (-1;10) ; (9;0) ; (-9;2) ; (3;-2) ; (-3;4)
15 tháng 4 2020
Do x.(y-1)=-9 nên: -9 chia hết cho x
=> x;(y-1) ước của 9
Ta có bảng gt sau:
x 1 -1 9 -9 3 -3
y-1 -9 9 -1 1 -3 3
y -8 10 0 2 -2 4
Vậy...
FG
1
15 tháng 5 2022
\(\Leftrightarrow x\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}\right)=\dfrac{1}{21}\)
\(\Leftrightarrow x\cdot\dfrac{2}{7}=\dfrac{1}{21}\)
hay \(x=\dfrac{1}{21}:\dfrac{2}{7}=\dfrac{1}{6}\)
HT
2
28 tháng 5 2017
11 - ( 15 + x ) = x - ( 25 - 9 )
\(\Rightarrow\)11 - 15 - x = x - 25 + 9
\(\Rightarrow\) - 4 - x = x - 16
\(\Rightarrow\)- x - x = - 16 + 4
\(\Rightarrow\) - 2x = -12
\(\Rightarrow\) x = 6
14 tháng 12 2016
a, nhân xét / x+2/ >= 0 với mọi x
dấu bằng xảy ra khi và chỉ khi
x+ 2= 0
=> x= -2
b, / x-5/ = /-7/
=> /x-5/= 7
xét 2 TH
TH1 / x-5/ = x-5
=> x-5 = 7
=> x= 12
TH2 / x-5/ = -(x-5) = -x+5 = 5-x
=> 5-x=7
=> x= -2
19 tháng 6 2017
xét xxxx=1111.x=11.101.x
vì 11 và 101 là 2 snt nên x ko thể là snt hay hợp số đc (nếu ko xxxx sẽ là tích của >= 3 snt)
lại có x khác 0 nên x=1 (1 và 0 là 2 số ko là snt hay hợp số )
vậy xxxx=1111 là số cần tìm
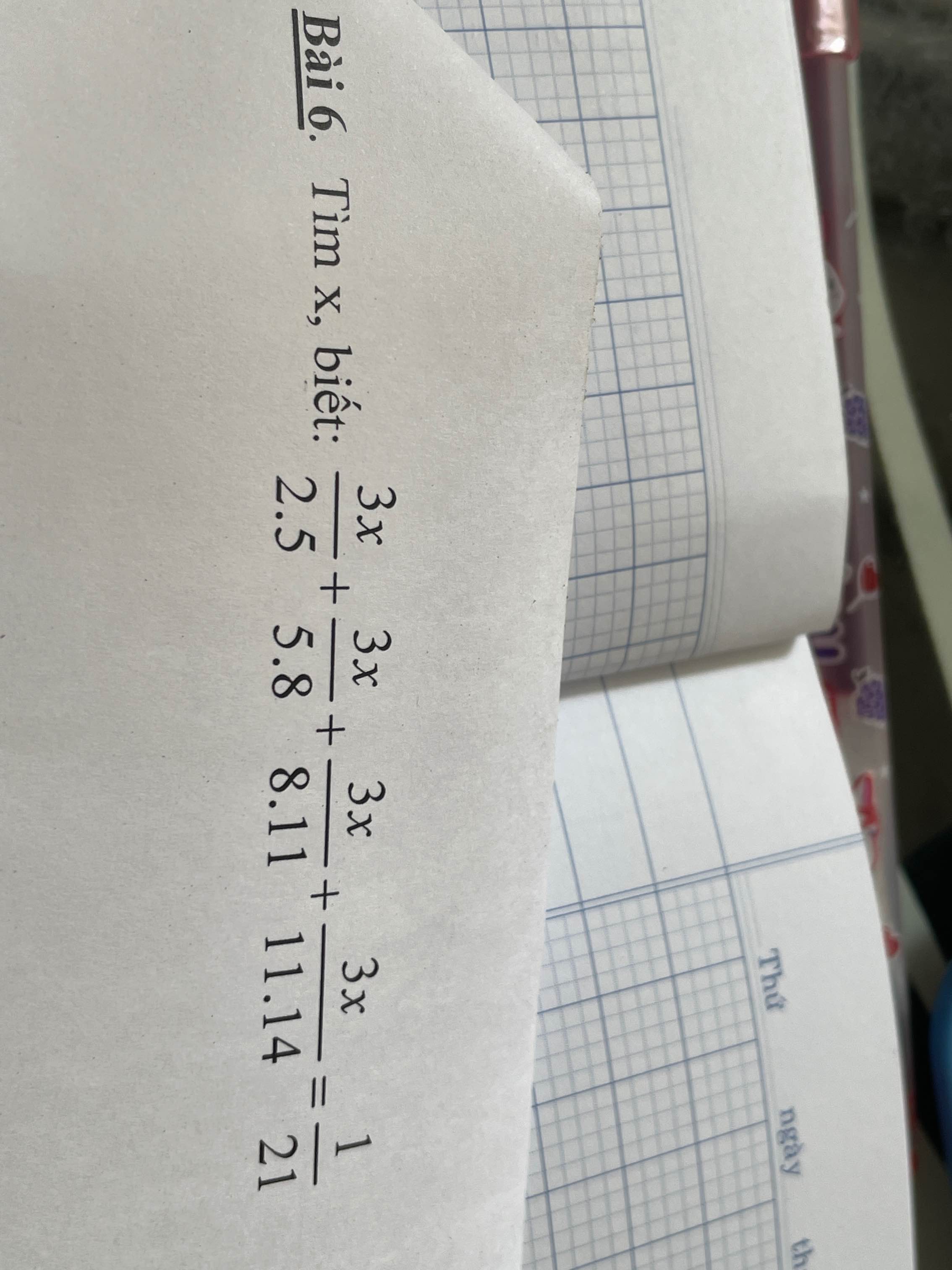
Ta có :
\(x^2-15x=0\)
\(\Leftrightarrow\)\(x\left(x-15\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=0\\x-15=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=15\end{cases}}}\)
Vậy \(x=0\) hoặc \(x=15\)
Chúc bạn học tốt ~
<=> \(x\left(x-15\right)=0\)
<=> \(\orbr{\begin{cases}x=0\\x=15\end{cases}}\)