K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
1 tháng 9 2018
Bài này cái khó là sử lý điều kiện thôi nên t làm phần đó thôi nhé.
Từ điều kiện suy ra được.
log\(\sqrt{3}\)(3x + 3y) + (3x + 3y) = log\(\sqrt{3}\)(x2 + y2 + xy + 2) + (x2 + y2 + xy + 2)
Dễ thấy hàm số f(t) = log\(\sqrt{3}\)(t) + t đồng biến trên (0; +\(\infty\)) nên
=> 3x + 3y = x2 + y2 + xy + 2
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2020
\(\Leftrightarrow\left(x+y\right)\left(x^2+y^2\right)=2\left(x+y\right)^2+2\left(x^2+y^2\right)+1\)
Đặt \(\left\{{}\begin{matrix}x+y=a\\x^2+y^2=b>0\end{matrix}\right.\) với \(a^2\le2b\)
\(\Rightarrow ab=2a^2+2b+1\)
\(\Leftrightarrow b\left(a-2\right)=2a^2+1\)
- Với \(a=2\) ko thỏa mãn
- Với \(a\ne2\Rightarrow b=\frac{2a^2+1}{a-2}=2\left(a+2\right)+\frac{9}{a-2}\)
\(\Rightarrow a-2=Ư\left(9\right)=\left\{-9;-1;1;9\right\}\Rightarrow a=\left\{-7;1;3;11\right\}\)
\(\Rightarrow b=\left\{-11;-3;19;27\right\}\)
Kết hợp điều kiện \(\left\{{}\begin{matrix}b\ge0\\a^2\le2b\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=19\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+y=3\\x^2+y^2=19\end{matrix}\right.\) ko tồn tại x, y nguyên thỏa mãn
27 tháng 2 2021
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y}\). khi đó gt trở thành:
\(a+b=a^2+b^2-ab\ge\dfrac{1}{4}\left(a+b\right)^2\Leftrightarrow o\le a+b\le4\);
\(A=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=\left(a+b\right)^2\le16\)
Đẳng thức xảy ra khi và chỉ khi a=b=2 <=> x=y=1/2
Vậy Max A = 16
PT
2
13 tháng 9 2019
Có: \(\left\{{}\begin{matrix}x^4+y^2\ge2x^{2y}\\x^2+y^4\ge2xy^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{x}{x^4+y^2}\le\frac{x}{2x^{2y}}\\\frac{y}{x^2+y^4}\le\frac{y}{2xy^2}\end{matrix}\right.\)
Mà xy = 1 \(\Rightarrow\left\{{}\begin{matrix}\frac{x}{2x^{2y}}=\frac{x}{2x}=\frac{1}{2}\\\frac{y}{2xy^2}=\frac{y}{2y}=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\frac{x}{x^4+y^2}+\frac{y}{x^2+y^4}\le\frac{1}{2}+\frac{1}{2}=1\)
Vậy GTLN của A = 1
\("="\Leftrightarrow x=y=1\)
P/s: Bài này em không chắc chắn lắm, nhờ chị Akai Haruma kiểm tra giúp ạ.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2019
\(xy=1\Rightarrow y=\frac{1}{x}\)
\(A=\frac{x}{x^4+\left(\frac{1}{x}\right)^2}+\frac{\frac{1}{x}}{x^2+\left(\frac{1}{x}\right)^4}=\frac{x^3}{x^6+1}+\frac{x^3}{x^6+1}=\frac{2x^3}{x^6+1}\le\frac{2x^3}{2\sqrt{x^6.1}}=\frac{2x^3}{2\left|x^3\right|}\le1\)
\(\Rightarrow A_{max}=1\) khi \(x=y=1\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 6 2019
ĐKXĐ: \(x\ne y\)
\(log_xy=\frac{1}{log_xy}\Leftrightarrow log_x^2y=1\Leftrightarrow\left[{}\begin{matrix}log_xy=1\\log_xy=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=y\left(l\right)\\x=\frac{1}{y}\end{matrix}\right.\)
\(log_x\left(x-\frac{1}{x}\right)=log_{x^{-1}}\left(x+\frac{1}{x}\right)\Leftrightarrow log_x\left(x-\frac{1}{x}\right)=-log_x\left(x+\frac{1}{x}\right)\)
\(\Leftrightarrow log_x\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=0\Leftrightarrow\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=1\)
\(\Leftrightarrow x^2-\frac{1}{x^2}=1\Leftrightarrow x^4-x^2-1=0\Rightarrow x^2=\frac{1+\sqrt{5}}{2}\Rightarrow y^2=\frac{1}{x^2}=\frac{-1+\sqrt{5}}{2}\)
\(\Rightarrow x^2+xy+y^2=\frac{1+\sqrt{5}}{2}+1+\frac{-1+\sqrt{5}}{2}=\sqrt{5}+1\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 8 2020
\(\left(x+y\right)xy=x^2+y^2-xy\)
\(\Leftrightarrow\left(x+y\right)xy=\left(x+y\right)^2-3xy\)
Đặt \(x+y=t\Rightarrow xy=\frac{t^2}{t+3}\)
Lại có \(\left(x+y\right)^2\ge4xy\Rightarrow t^2\ge\frac{4t^2}{t+3}\)
\(\Leftrightarrow t^2\left(\frac{t-1}{t+3}\right)\ge0\Rightarrow\left[{}\begin{matrix}t\ge1\\t< -3\end{matrix}\right.\)
\(A=\frac{x^3+y^3}{\left(xy\right)^3}=\frac{\left(x+y\right)\left(x^2+y^2-xy\right)}{\left(xy\right)^3}=\frac{\left(x+y\right)\left(x+y\right)xy}{\left(xy\right)^3}=\left(\frac{x+y}{xy}\right)^2\)
\(A=\left(\frac{t\left(t+3\right)}{t^2}\right)^2=\left(\frac{t+3}{t}\right)^2=\left(1+\frac{3}{t}\right)^2\)
\(\Rightarrow y'=-\frac{6\left(t+3\right)}{t^3}< 0\) \(\forall t\ge1;t< -3\)
\(\lim\limits_{x\rightarrow-\infty}\left(1+\frac{3}{t}\right)^2=1\Rightarrow A_{max}=A\left(1\right)=16\)
\(\Rightarrow M=16\) khi \(x=y=\frac{1}{2}\)
HN
2
B
3 tháng 9 2021
Từ gt ta có x^2+y^^2=xy+1
=>P=(x^2+y^2)^2-2x^2y^2-x^2y^2
=(xy+1)2-2x2y2-x2y2
=x2y2+xy+1-3x2y2=-2x2y2+xy+1
=......
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
\(1=x^2+y^2-xy\ge2xy-xy=xy\Rightarrow xy\le1\)
\(1=x^2+y^2-xy\ge-2xy-xy=-3xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(\Rightarrow-\dfrac{1}{3}\le xy\le1\)
\(P=\left(x^2+y^2\right)^2-2\left(xy\right)^2-\left(xy\right)^2=\left(xy+1\right)^2-3\left(xy\right)^2=-2\left(xy\right)^2+2xy+1\)
Đặt \(xy=t\in\left[-\dfrac{1}{3};1\right]\)
\(P=f\left(t\right)=-2t^2+2t+1\)
\(f'\left(t\right)=-4t+2=0\Rightarrow t=\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow P_{max}=\dfrac{3}{2}\) ; \(P_{min}=\dfrac{1}{9}\)
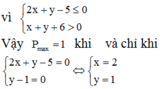
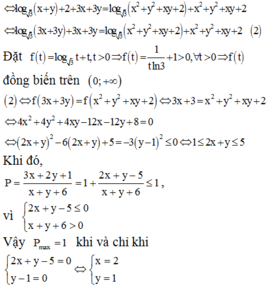
Đề không rõ ràng. Bạn xem lại.