Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left(x\right)=3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(f\left(-1\right)=-2;f\left(0\right)=2;f\left(2\right)=-2\)
\(\Rightarrow M=2;m=-2\Rightarrow P=6\)
Cả 4 đáp án đều sai (kiểm tra lại đề bài, có đúng là \(f\left(x\right)=x^3-3x^2+2\) hay không?)

3.
\(y'=-3x^2-6x=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=0\end{matrix}\right.\)
\(y\left(-1\right)=m-2\) ; \(y\left(1\right)=m-4\)
\(\Rightarrow y_{min}=y\left(1\right)=m-4\)
\(\Rightarrow m-4=0\Rightarrow m=4\)
4.
Hàm đã cho bậc nhất trên bậc nhất nên đơn điệu trên mọi khoảng xác định
\(\Rightarrow y_{min}+y_{max}=y\left(1\right)+y\left(2\right)=\frac{m+1}{2}+\frac{m+2}{3}=8\)
\(\Rightarrow m=\frac{41}{5}\)
Đáp án B
1.
\(y'=\frac{1}{\left(sinx+1\right)^2}.cosx>0\Rightarrow y\) đồng biến
\(m=y_{min}=y\left(0\right)=2\)
\(M=y_{max}=y\left(1\right)=\frac{5}{2}\)
\(\Rightarrow M^2+m^2=\frac{41}{4}\)
2.
Hàm xác định trên \(\left[-2;2\right]\)
\(y'=1-\frac{x}{\sqrt{4-x^2}}=0\Leftrightarrow x=\sqrt{2}\)
\(y\left(-2\right)=-2\) ; \(y\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(y\left(2\right)=2\)
\(\Rightarrow N=-2;M=2\sqrt{2}\)
\(\Rightarrow M+2N=2\sqrt{2}-4\)

Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
![]()
![]() (do
x
2
+
y
2
=
2
)
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
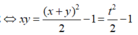
Từ ![]()
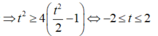
P = f(t) 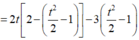
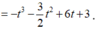
Xét f(t) trên [-2;2].
Ta có ![]()
Bảng biến thiên
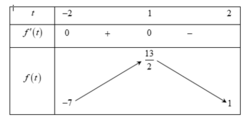
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có ![]()
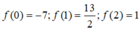
Suy ra kết luận.

1/ \(f'\left(x\right)=\frac{3\sqrt{x^2+1}-\frac{x\left(3x+1\right)}{\sqrt{x^2+1}}}{x^2+1}=\frac{3\left(x^2+1\right)-3x^2-x}{\left(x^2+1\right)\sqrt{x^2+1}}=\frac{3-x}{\left(x^2+1\right)\sqrt{x^2+1}}\)
Hàm số đồng biến trên \(\left(-\infty;3\right)\) nghịch biến trên \(\left(3;+\infty\right)\)
\(\Rightarrow f\left(x\right)\) đạt GTLN tại \(x=3\)
\(f\left(x\right)_{max}=f\left(3\right)=\frac{10}{\sqrt{10}}=\sqrt{10}\)
2/ \(y'=\frac{\sqrt{x^2+2}-\frac{\left(x-1\right)x}{\sqrt{x^2+2}}}{x^2+2}=\frac{x^2+2-x^2+x}{\left(x^2+2\right)\sqrt{x^2+2}}=\frac{x+2}{\left(x^2+2\right)\sqrt{x^2+2}}\)
\(f'\left(x\right)=0\Rightarrow x=-2\in\left[-3;0\right]\)
\(y\left(-3\right)=-\frac{4\sqrt{11}}{11}\) ; \(y\left(-2\right)=-\frac{\sqrt{6}}{2}\) ; \(y\left(0\right)=-\frac{\sqrt{2}}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}M=-\frac{\sqrt{2}}{2}\\N=-\frac{\sqrt{6}}{2}\end{matrix}\right.\) \(\Rightarrow MN=\frac{\sqrt{12}}{4}=\frac{\sqrt{3}}{2}\)
Tất cả các đáp án đều sai
3/ \(\left\{{}\begin{matrix}\left|x-3\right|\ge0\\\sqrt{x+1}>0\end{matrix}\right.\) \(\Rightarrow f\left(x\right)\ge0\) \(\forall x\Rightarrow N=0\) khi \(x=3\)
- Với \(0\le x< 3\Rightarrow f\left(x\right)=\left(3-x\right)\sqrt{x+1}\)
\(\Rightarrow f'\left(x\right)=-\sqrt{x+1}+\frac{\left(3-x\right)}{2\sqrt{x+1}}=\frac{-2\left(x+1\right)+3-x}{2\sqrt{x+1}}=\frac{-3x+1}{2\sqrt{x+1}}\)
\(f'\left(x\right)=0\Rightarrow x=\frac{1}{3}\)
- Với \(3< x\le4\Rightarrow f\left(x\right)=\left(x-3\right)\sqrt{x+1}\)
\(\Rightarrow f'\left(x\right)=\sqrt{x+1}+\frac{x-3}{2\sqrt{x+1}}=\frac{2\left(x+1\right)+x-3}{2\sqrt{x+1}}=\frac{3x-1}{2\sqrt{x+1}}>0\) \(\forall x>3\)
Ta có: \(f\left(0\right)=3\) ; \(f\left(\frac{1}{3}\right)=\frac{16\sqrt{3}}{9}\) ; \(f\left(4\right)=\sqrt{5}\)
\(\Rightarrow M=\frac{16\sqrt{3}}{9}\Rightarrow M+2N=\frac{16\sqrt{3}}{9}\)
Câu 2 hình như câu B mà người ta nói đạt GTLN . GTNN tại M , N nên là 0 x -2 =0

Đáp án A
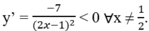
Suy ra hàm nghịch biến trên từng khoảng xác định, do đó hàm số nghịch biến trên đoạn [1; 4]. Vậy m = y(4) = 1; M = y(1) = 4 => d = M – m = 4 – 1 = 3

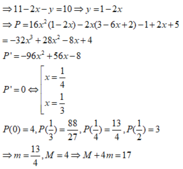
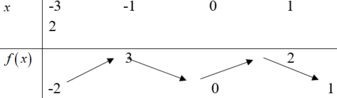



Đáp án C