Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=3\)
a. \(\overrightarrow{IM}=\left(0;2\right)\Rightarrow IM=\sqrt{0^2+2^2}=2< R\Rightarrow\) M nằm trong đường tròn
b. \(d\left(I;d\right)=\dfrac{\left|2-\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=2\sqrt{2}< 3\Rightarrow d\) cắt đường tròn tại 2 điểm
c. Khoảng cách giữa 2 điểm trên đường tròn là lớn nhất khi chúng nằm ở 2 mút đường kính
\(\Rightarrow\) d' đi qua tâm I
Do d' vuông góc d nên nhận (1;1) là 1 vtpt
Phương trình: \(1\left(x-2\right)+1\left(y+1\right)=0\Leftrightarrow x+y-1=0\)

Đáp án: A
Ta có:
(C): x 2 + y 2 - 4x + 2y + 1 = 0 ⇔ (x - 2 ) 2 + (y + 1 ) 2 = 4
⇒ I(2;-1), R = 2
Ta thấy:
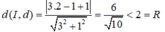
Suy ra, d cắt đường tròn (C) tại hai điểm phân biệt
Thay tọa độ của I vào vế trái phương trình đường thẳng d ta được: 3.2 - 1 + 1 = 6 ≠ 0
Suy ra, I không thuộc d