Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(\alpha_1\right)\)//\(\left(\alpha'_1\right)\)
b) \(\left(\alpha_2\right)\) cắt \(\left(\alpha'_2\right)\)
c) \(\left(\alpha_3\right)\) trùng với \(\left(\alpha'_3\right)\)

a) Hai mặt phẳng cắt nhau, vì 1: 2: (-1) ≠ 2: 3: (-7)
b) Hai mặt phẳng cắt nhau, vì: 1: (-2): 1 ≠ 2: (-1): 4
c) Hai mặt phẳng song song, vì: 1/2=1/2=1/2 ≠ -1/3
d) Hai mạt phẳng cắt nhau, vì: 3: (-2): 3 ≠ 9: (-6): (-9)
e) Hai mặt phẳng trung nhau, vì: 1/10=-1/(-10)=2/20=-4/(-40).
#rin

Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng ( α ) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0
⇔ 4t = 0 ⇔ t = 0
Vậy đường thẳng d cắt mặt phẳng ( α ) tại M 0 (0; 1; 1)

Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của ( α ) ta được: (2 – t) +(2 + t) + 5 = 0 ⇔ 0t = -9
Phương trình vô nghiệm, vậy đường thẳng d song song với ( α )

Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:
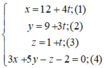
Thay (1); (2); (3) vào (4) ta được:
3(12 + 4t) + 5(9 + 3t) – (1 + t) – 2 = 0
⇔ 36 + 12t + 45 + 15t – 1 – t – 2 = 0
⇔ 26t + 78 = 0
⇔ t = -3
Vậy (d) cắt (α) tại một điểm M(0 ; 0 ; -2).

Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của ( α ) ta được: (3 – t) + (2 – t) + (1 + 2t) – 6 = 0 ⇔ 0t = 0
Phương trình luôn thỏa mãn với mọi t. Vậy d chứa trong ( α ) .

n → α = (1;-2;3); n → β = (2;-4;6)
Hai vecto pháp tuyến của hai mặt phẳng là hai vecto tỉ lệ
( α 1 ) // ( α ' 1 )