
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


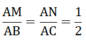
⇒ MN // BC (định lí Ta lét đảo)
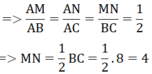
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).
Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)
Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).

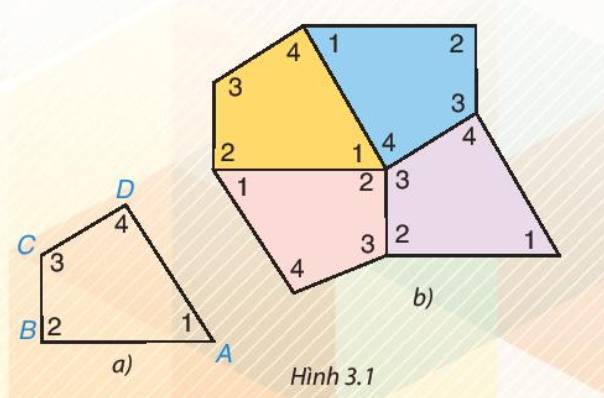
- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)

a)
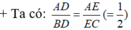
Nên theo định lí ta- let đảo ta có: DE // BC.
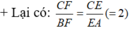
Nên theo định lí ta- let đảo ta có: EF // AB.
b) Tứ giác BDEF là hình bình hành vì có các cặp cạnh đối song song với nhau
c) Tứ giác BDEF là hình bình hành ⇒ DE = BF = 7
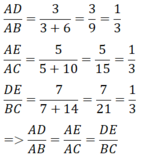
Ba cạnh của ΔADE tương ứng tỉ lệ với ba cạnh của ΔABC

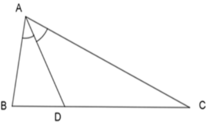
Vì AD là đường phân giác của tam giác ABC nên: A B A C = B D D C
Theo bài, ta có: AC = 2AB ⇒ A B A C = 1 2 ⇒ B D D C = 1 2 hay (I) đúng
Lại có: B D D C = 1 2 ⇒ B D B C = B D D C + B D = 1 2 + 1 = 1 3 nên (III) sai.
⇒ D C B C = B C − B D B C = 1 − B D B C = 1 − 1 3 = 2 3
hay (II) đúng
Vậy chỉ có 2 khẳng định đúng.
Đáp án: D
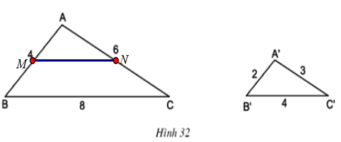
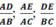 và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.
và cho nhận xét về mối liên hệ giữa các cặp cạnh tương ứng của hai tam giác ADE và ABC.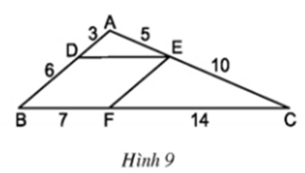
BẠN HỎI LÀM J
*THẮC CMN MẮC*
Là comment nha bn!
Tk mk nha!