
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1: TXĐ: D=R\{3}
\(y=\dfrac{x^2-6x+10}{x-3}\)
=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)
Đặt y'<=0
=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)
=>\(x^2-6x+8< =0\)
=>(x-2)(x-4)<=0
=>2<=x<=4
Vậy: Khoảng đồng biến là [2;3) và (3;4]

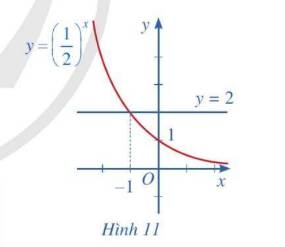
Do \(\dfrac{1}{2}< 1\) ⇒ Hàm số \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R.
\(\left(\dfrac{1}{2}\right)^x>2\\ \Rightarrow x< log_{\dfrac{1}{2}}2\\ \Rightarrow x< -1\)

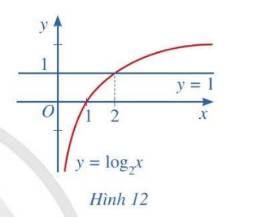
Do 2 > 1 ⇒ hàm số y = log2x đồng biến trên D = \(\left(0;+\infty\right)\)
\(log_2x>1\\ \Rightarrow x>2\)

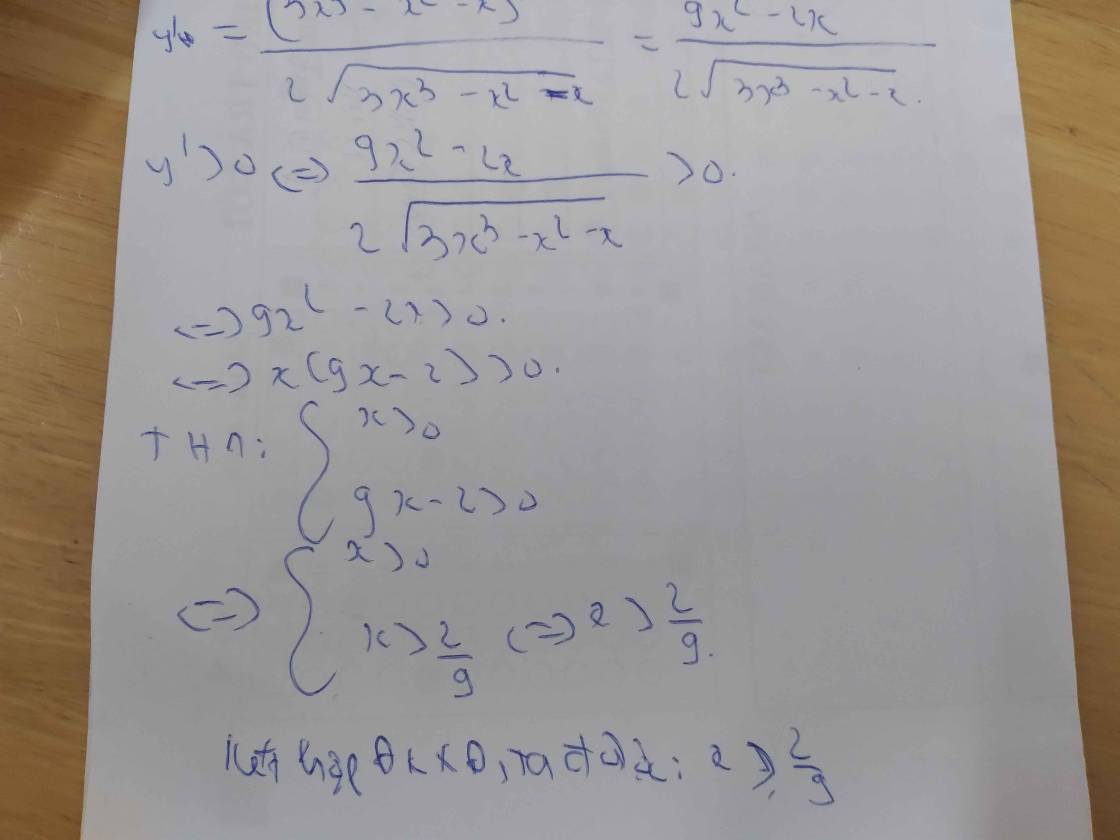

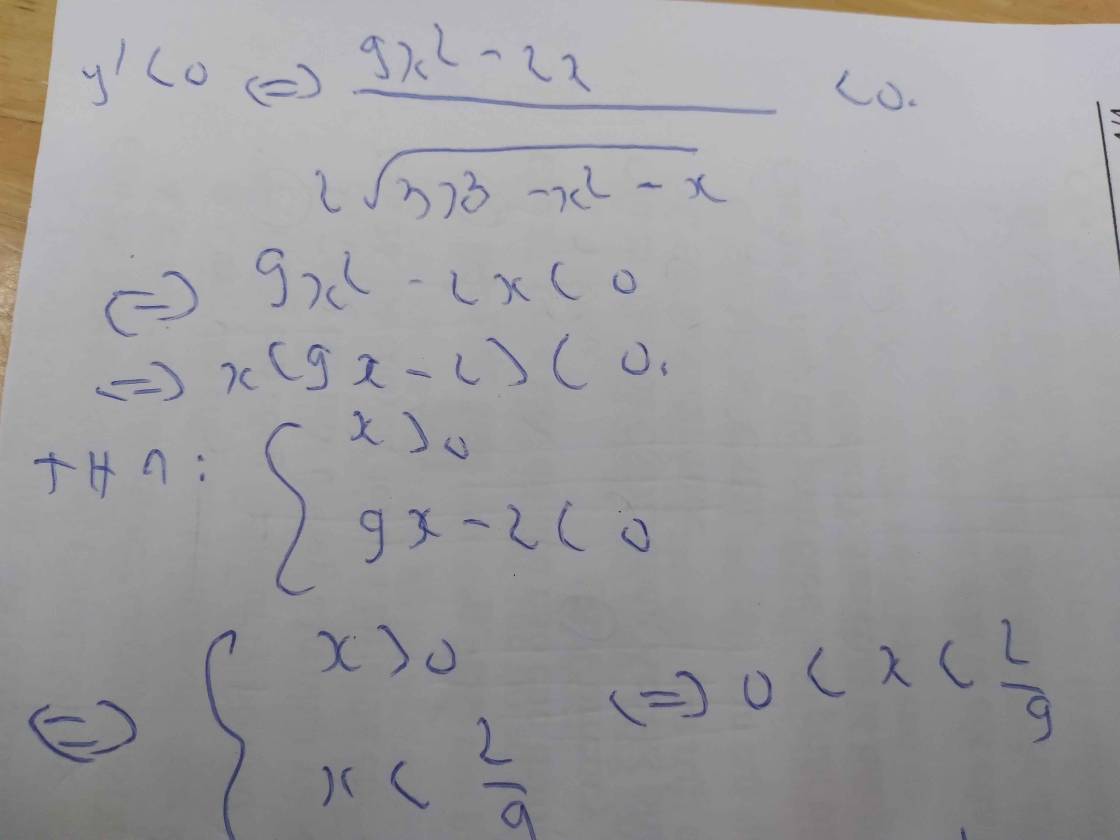
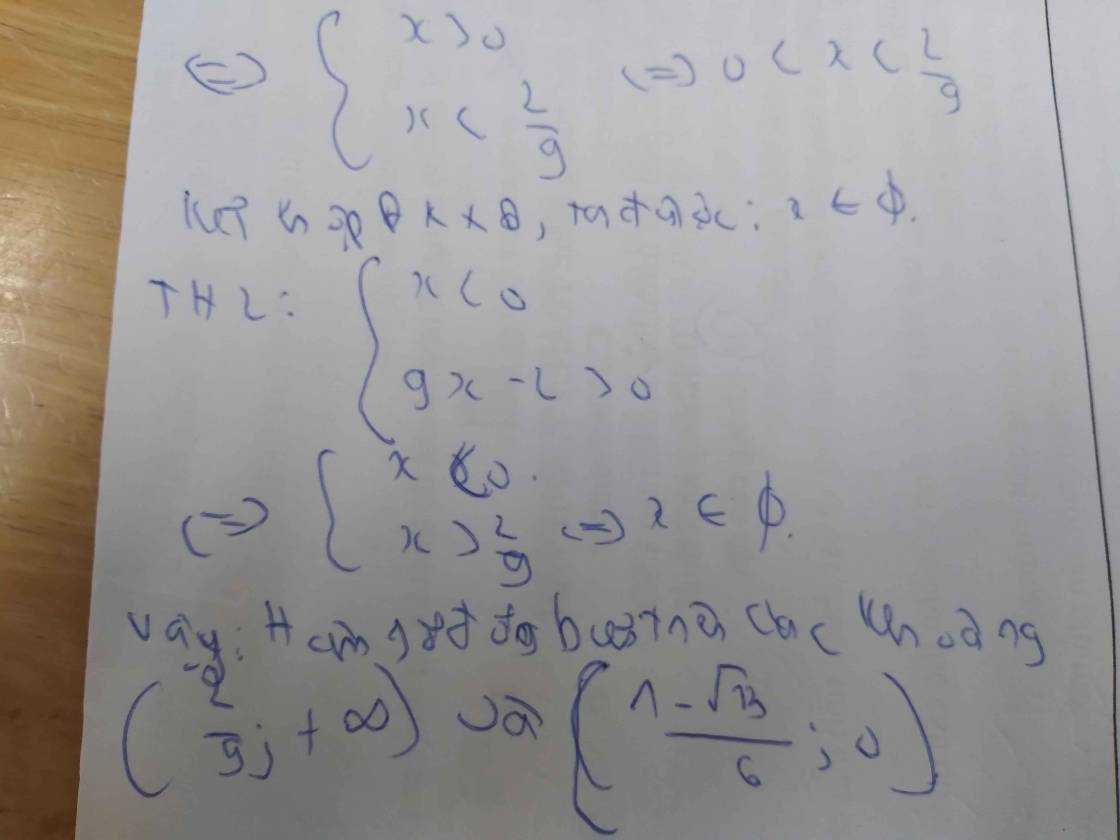





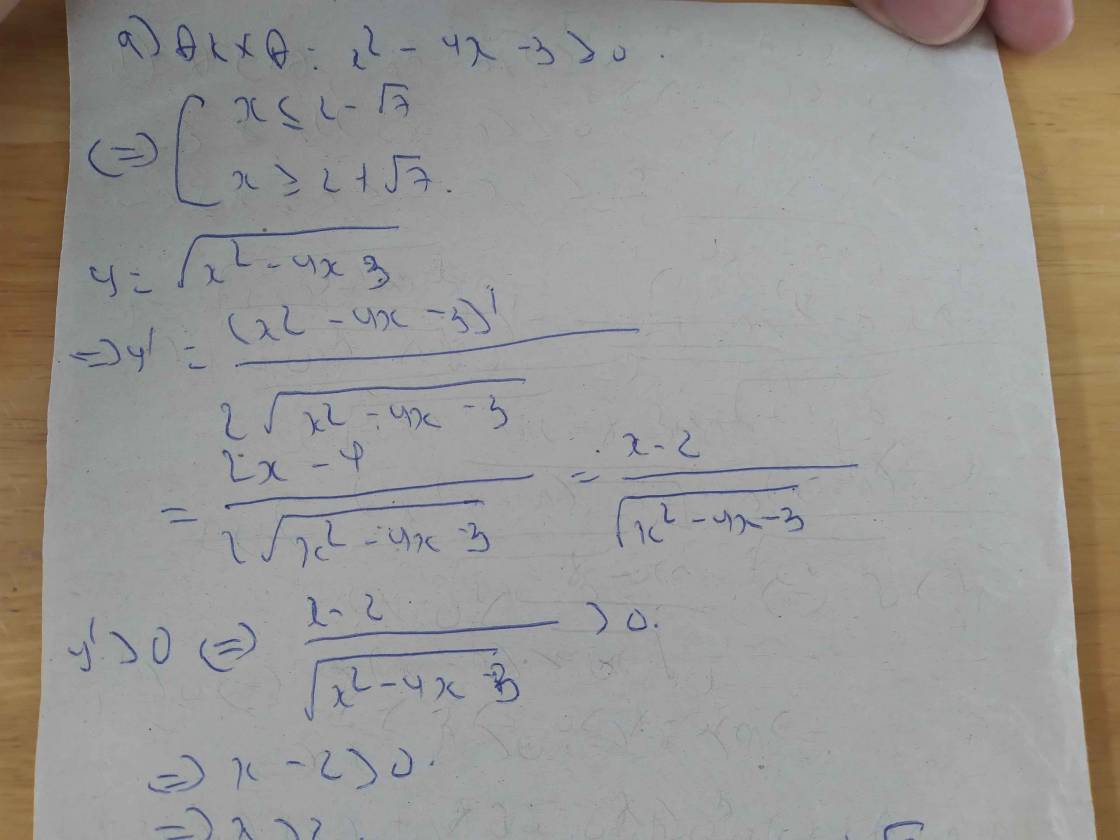


























ĐKXĐ: \(x^2-6x+5>=0\)
=>(x-1)(x-5)>=0
TH1: \(\left\{{}\begin{matrix}x-1>=0\\x-5>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=1\\x>=5\end{matrix}\right.\Leftrightarrow x>=5\)
TH2: \(\left\{{}\begin{matrix}x-1< =0\\x-5< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =1\\x< =5\end{matrix}\right.\)
=>x<=1
\(y=\sqrt{x^2-6x+5}\)
=>\(y'=\dfrac{\left(x^2-6x+5\right)'}{2\sqrt{x^2-6x+5}}\)
=>\(y'=\dfrac{2x-6}{2\sqrt{x^2-6x+5}}\)
Đặt y'>0
=>\(\dfrac{2x-6}{2\sqrt{x^2-6x+5}}>0\)
=>2x-6>0
=>x>3
kết hợp ĐKXĐ, ta được: x>5
Đặt y'<0
=>\(\dfrac{2x-6}{2\sqrt{x^2-6x+5}}< 0\)
=>2x-6<0
=>x<3
Kết hợp ĐKXĐ, ta được: x<1
Vậy: Hàm số nghịch biến trên (-\(\infty\);1) và đồng biến trên (5;+\(\infty\))