TT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Hàm số \(y = \sin 2x + \tan 2x\) có nghĩa khi \(tan 2x\) có nghĩa
\(\cos 2x \ne 0\;\; \Leftrightarrow 2x \ne \frac{\pi }{2}\;\;\;\; \Leftrightarrow x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}\) \
Vây tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - 2x} \right) + \tan \left( { - 2x} \right) = - \sin 2x - \tan 2x = - \left( {\sin 2x + \tan 2x} \right) = - f\left( x \right),\;\forall x \in D\).
Vậy \(y = \sin 2x + \tan 2x\) là hàm số lẻ
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cos \left( { - x} \right) + {\sin ^2}\left( { - x} \right) = \cos x + {\sin ^2}x = f\left( x \right),\;\forall x \in D\)
Vậy \(y = \cos x + {\sin ^2}x\) là hàm số chẵn
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
c) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right)\cos \left( { - 2x} \right) = - \sin x.\cos 2x = - f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x\cos \;2x\) là hàm số lẻ
d) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) + \cos \left( { - x} \right) = - \sin x + \cos x \ne f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x + \cos x\) không là hàm số chẵn cũng không là hàm số lẻ
NT
0
CM
15 tháng 1 2017
Đáp án D
Ta có tập xác định D = R.
Hàm số y = f(x) = 0 có:
f(-x) = 0 và –f(x) = 0
=> f(x) = f(-x) = -f(x) vừa thỏa mãn tính chất của hàm số chẵn, vừa thỏa mãn tính chất của hàm số lẻ, nên đây là hàm số vừa chẵn vừa lẻ.
BT
0
BT
1
C
5 tháng 9 2016
a) y = sinx - cosx
Đặt \(f\left(x\right)\) = y = sinx - cosx
Ta có : \(f\left(-x\right)=sin\left(-x\right)-cos\left(-x\right)\)
<=> \(f\left(-x\right)=-sinx+cosx\)
<=> \(f\left(-x\right)\ne f\left(x\right)\)
Vậy hàm số đã cho là hàm số không chẵn , không lẻ .
b) y = sinxcos2x + tanx
y = \(f\left(x\right)=sinxcos^2x+tanx\)
TXĐ : \(D_1=R\backslash\left\{\frac{\pi}{2}+k\pi\left|k\in Z\right|\right\}\)
Vì với mọi x \(\in\) D1 , ta có - x \(\in\) D1
và \(f\left(-x\right)=sin\left(-x\right)cos^2\left(-x\right)+tan\left(-x\right)\)
\(=-sinxcos^2x-tanx=-f\left(x\right)\)
Nên hàm số đã cho là hàm số lẻ
6 tháng 9 2016
cô ơi , tại sao lại không thể biến đổi \(-\sin x+\cos x\) thành \(-\left(\sin x-\cos x\right)\)?
BT
0
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Ta có:
\(\left. \begin{array}{l}f\left( { - x} \right) = \sin \left( { - x} \right).\cos \left( { - x} \right) = - \sin x.\cos x\\f\left( x \right) = \sin x.\cos x\end{array} \right\} \Rightarrow f\left( { - x} \right) = - f\left( x \right)\)
Hàm số \(y = \sin x\cos x\) là hàm số lẻ
b) Ta có:
\(\left. \begin{array}{l}f\left( { - x} \right) = \tan \left( { - x} \right) + \cot \left( { - x} \right) = - \tan x - \cot x\\f\left( x \right) = \tan x + \cot x\end{array} \right\} \Rightarrow f\left( { - x} \right) = - f\left( x \right)\)
Hàm số \(y = \tan x + \cot x\) là hàm số lẻ
c) Ta có:
\(\left. \begin{array}{l}f\left( { - x} \right) = {\sin ^2}\left( { - x} \right) = {\left( { - \sin \left( x \right)} \right)^2} = {\sin ^2}x\\f\left( x \right) = {\sin ^2}x\end{array} \right\} \Rightarrow f\left( { - x} \right) = f\left( x \right)\)
Hàm số \(y = {\sin ^2}x\) là hàm số chẵn
HP
26 tháng 9 2021
a, \(f\left(-x\right)=sin^2\left(-2x\right)+cos\left(-3x\right)=sin^22x+cos3x=f\left(x\right)\)
\(\Rightarrow\) Là hàm số chẵn.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
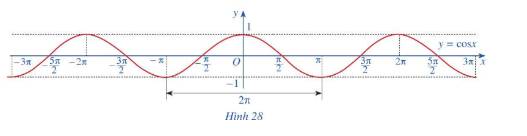
a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)
Tập xác định: \(D=ℝ\).
Với \(x\in D\)thì \(-x\in D\).
\(f\left(x\right)=cos\left(x+1\right)+cos\left(x-1\right)\)
\(f\left(-x\right)=cos\left(-x+1\right)+cos\left(-x-1\right)\)
\(=cos\left[-\left(x-1\right)\right]+cos\left[-\left(x+1\right)\right]\)
\(=cos\left(x-1\right)+cos\left(x+1\right)=f\left(x\right)\)
Do đó hàm số \(y=cos\left(x+1\right)+cos\left(x-1\right)\)là hàm chẵn.