Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
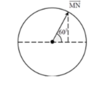
Vecto quay OM→ có:
+ Có độ lớn bằng hai đơn vị chiều dài nên biên độ dao động A = 2.
+ Quay quanh O với tốc độ góc 1 rad/s nên tần số ω = 1rad/s.
+ Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o nên pha ban đầu là φ = π/6 rad.
Phương trình dao động: x = 2.cos(t + π/6).

Phương trình tổng quát: x = Acos(ωt + φ).
+ Biên độ: A = 2 đơn vị chiều dài.
+ Tần số góc: ω = 1rad/s.
+ Pha ban đầu: φ = 300 = .
Vậy đáp án đúng là : B
B. Phương trình tổng quát: x = Acos(ωt + φ).
+ Biên độ: A = 2 đơn vị chiều dài.
+ Tần số góc: ω = 1rad/s.
+ Pha ban đầu: φ = 300 = .

Dao động này có biên độ \(A=5cm\)
Tần số góc là \(5\pi\left(rad/s\right)\)
Chu kì \(T=\dfrac{2\pi}{\omega}=0,4s\)
Và tần số là: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
⇒ Chọn B

Hướng dẫn: Chọn đáp án B
Kinh nghiệm: Bài toán cho x1 và xu hướng đang tăng (v1 > 0) hoặc đang giảm (v1 <0) thì nên làm theo cách 2.
Cách 1: Viết lại phương trình li độ vận tốc:
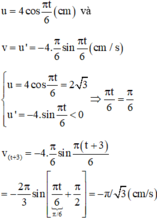
Cách 2: Chọn trạng thái tại thời điểm t1 là trạng thái ban đầu Þj= p/6 Pha dao động ở thời điểm tiếp theo:
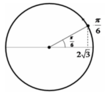
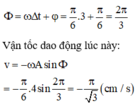

Phương trình tổng quát: \(x= A cos(\omega t+\varphi)\)
+ Tần số góc: \(\omega = 2\pi/2 = \pi \ (rad/s)\)
+ t=0, vật qua VTCB theo chiều đương \(\Rightarrow\left\{ \begin{array}{} x_0 = 0\ cm\\ v_0 >0 \end{array} \right.\)\(\Rightarrow\left\{ \begin{array}{} \cos \varphi = 0\ cm\\ \sin \varphi <0 \end{array} \right. \Rightarrow \varphi = -\frac{\pi}{2}\)
Vậy phương trình dao động: \(x = 5\cos(\pi t - \frac{\pi}{2})\) (cm)
tại sao lại ra φ=\(\dfrac{-\pi}{2}\) làm cách nào vậy bạn???
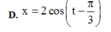


Đáp án B
+ Vecto quay OM → biểu diễn dao động: x = 2 cos t + π 3