Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
\(W_1=2W_2\Rightarrow A_1=A_2\sqrt{2}=a\sqrt{2}\)
Đặt \(A_{23}=x\) thì: \(x_{23}\perp x_1\rightarrow x_{23}\perp x_2\Rightarrow A_3=\sqrt{x^2+a^2}\)
Ta lại có: \(A_{13}=\sqrt{A_1^2+A^2_3+2A_1A_3\cos\left(x_1;x_3\right)}\)
Trong đó: \(\cos\left(x_1;x_3\right)=-\cos\left(x_2;x_3\right)=\dfrac{a}{\sqrt{x^2+a^2}}\)
Do đó: \(A_{13}=\sqrt{x^2+3a^2+2\sqrt{2}a^2}\)
Kết hợp với giả thiết ta có:
\(3=\dfrac{W_{13}}{W_{23}}=\left(\dfrac{A_{13}}{A_{23}}\right)^2=\dfrac{x^2+3a^2+2\sqrt{2}a^2}{x^2}\)
\(\Rightarrow x=\dfrac{\sqrt{2}+1}{\sqrt{2}}a\)
Do \(x_{23}\perp x_1\) nên:
\(A_{th}=\sqrt{A^2_{23}+A^2_1}=\sqrt{2a^2+\dfrac{3+2\sqrt{2}}{2}a^2}\) \(=\dfrac{7+2\sqrt{2}}{\sqrt{2}}a\)
\(\Rightarrow\dfrac{W_{th}}{W_{23}}=\left(\dfrac{A_{th}}{A_{23}}\right)^2=...=\dfrac{7+2\sqrt{2}}{\sqrt{2}+1}\approx1,7\)
Vậy ta chọn \(D\)

Đáp án B
Phương pháp: Sử dụng công thức tính cơ năng của con lắc đơn dao động điều hoà
W = (1/2)mglα02

1. Biểu diễn bằng véc tơ quay, trong thời gian T/6 thì véc tơ quay góc: 360/6 = 600
Vật đạt tốc độ cực đại khi nó đi qua VTCB, ta có:
Như vậy, quãng đường vật đi trong T/6 là: A/2 + A/2 = A.
Tốc độ trung bình cực đại: \(v=\frac{S}{t}=\frac{A}{\frac{T}{6}}=6\frac{A\omega}{2\pi}=\frac{3.A.4\pi}{2\pi}=60\)\(\Rightarrow A=10\)cm
2. Biên độ A = 10/2 = 5cm.
Khi vật có Wd = 0,009 J thì thế năng: \(W_t=W-W_đ=\frac{1}{2}.20.0,05^2-0,009=0,016\)J
Suy ra: \(\frac{1}{2}.20.x^2=0,016\Rightarrow x=4\)cm
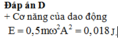
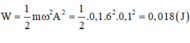

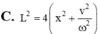


Đáp án A
+ Cơ năng của con lắc E = 1 2 mω 2 A 2 = 1 2 mω 2 L 2 2 = 1 8 mω 2 L 2