Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của 2 xe xuất phát tại A,B lần lượt là vA và vB
Lượt đi, 2 xe gặp nhau tại vị trí cách B 50km, cách A 70km nên \(\frac{v_A}{v_B}=\frac{70}{50}=\frac{7}{5}\)
Gọi lượt về 2 xe gặp nhau tại vị trí cách A là x(km)
Quãng đường xe từ A đi đc là 2AB-x=240-x
Quãng đường xe từ B đi đc là AB+x=120+x
ta có \(\frac{240-x}{120+x}=\frac{7}{5}\)
\(\Rightarrow\)x=30(km)
vậy cách A là 30km (hơi dài, mà thôi nhác nghĩ quá)
chúc bạn học tốt
HYC-24/1/2022

Gọi vận tốc của ô tô là x (km/h) (x > 0)
Vì hai xe cùng xuất phát nên khi hai xe gặp nhau thì thời gian đi của hai xe là bằng nhau và khi đó ô tô đi được 75 km còn xe máy đi được 45 km
Thời gian ô tô và xe máy đi cho đến khi gặp nhau là 75/x (h)
Vận tốc của xe máy là: 45 : 75 x = 3 x 5 (km/h)
Nếu xe máy đi trước ô tô 48 phút =4/5 h thì quãng đường đi được của 2 xe bằng nhau và bằng 60km
Thời gian đi quãng đường 60km của ô tô là: 60/x h
Thời gian đi quãng đường 60km của xe máy là: 60 : 3 x 5 = 100 x
Theo bài ra ta có phương trình: 100 x - 60 x = 4 5 ⇔ 40 x = 4 5 ⇔ x = 50 (TM)
Vậy vận tốc của ô tô là 50 km/h, vận tốc của xe máy là 30 km/h
Đáp án: B

Gọi vận tốc ô tô đi từ \(A:a\)
Gọi vận tốc ô tô đi từ \(B:b\)
Vì xe máy khởi hành trước ô tô 48 phút thì sẽ gặp nhau ở giữa quãng đường
\(\Rightarrow a>b\)
\(\Rightarrow AC=75km\) và \(BC=120-75=45km\)
\(\Rightarrow\frac{75}{a}=\frac{45}{b}\)
\(\Rightarrow a=\frac{75.b}{45}\)
Thời gian xe ô tô đi hết nữa quảng đường là: \(\frac{120:2}{a}=\frac{60}{a}\)
\(\Rightarrow b.0,8+b.\frac{60}{a}=60\)
\(\Rightarrow b.0,8+.+\frac{60}{\frac{75.b}{45}}=60\)
\(\Rightarrow b.0,8+36=60\)
\(\Rightarrow b=30\)
\(\Rightarrow a=50\)
Vậy ...................

Bài 1 :
Do a,b,c là 3 cạnh của một tam giác nên ta có các bđt
\(\hept{\begin{cases}a+b>c\\b+c>a\\c+a>b\end{cases}}\)
Do tính lớn nhỏ của căn bậc 2 và số trong nó liên hệ vs nhau nên
\(\hept{\begin{cases}\sqrt{a}+\sqrt{b}>\sqrt{c}\\\sqrt{b}+\sqrt{c}>\sqrt{a}\\\sqrt{c}+\sqrt{a}>\sqrt{b}\end{cases}}\)
Vậy \(\sqrt{a},\sqrt{b}\) và\(\sqrt{c}\) lập thành 3 cạnh của một tam giác.
Bài 2 :
Gọi thời gian người thứ nhất đi là xx(h), khi đó thời gian người thứ hai đi là x−1(h).
Vậy quãng đường người thứ nhất và người thứ hai đi đc lần lượt là 15x(km) và 35(x−1)(km).
Do khoảng cách hai xe cách nhau 90km, mà hai người đi 2 đường vuông góc, nên theo Pytago ta có
\(\left(15x\right)^2+\left[35\left(x-1\right)\right]^2=90^2\)
\(\Leftrightarrow225x^2+1225\left(x^2-2x+1\right)=8100\)
\(\Leftrightarrow1450x^2-2450x-6875=0\)
\(\Leftrightarrow58x^2-98x-275=0\)
Vậy : \(x=\frac{49+\sqrt{18351}}{58}\)
Do đó sau : \(\frac{49+\sqrt{18351}}{58}\approx190,83'\) thì hai người cách nhau 90(km)
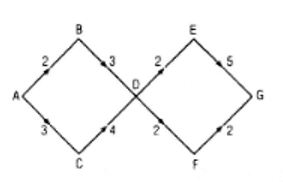
Có 4 phương án đi qua các tỉnh A đến G là:
a) A → B → D → E → G
b) A → B → D → F → G
c) A → C → D → E → G
d) A → C → D → F → G
Theo quy tắc nhân ta có:
Phương án a) có 2.3.2.5 = 60 cách đi
Phương án b) có 2.3.2.2 = 24 cách đi
Phương án c) có 3.4.2.5 = 120 cách đi
Phương án d) có 3.4.2.2 = 48 cách đi
Vậy theo quy tắc cộng có 60 + 24 + 120 + 48 = 252 cách đi từ A đến G.
Có 4 phương án đi qua các tỉnh A đến G là :
a. A → B → D → E → G
b. A → B → D → F → G
c. A → C → D → E → G
d. A → C → D → F → G
Theo quy tắc nhân, ta có :
Phương án a có 2.3.2.5=60 cách đi;
Phương án b có 2.3.2.2=24 cách đi;
Phương án c có 3.4.2.5=120 cách đi;
Phương án d có 3.4.2.2=48 cách đi.
Theo quy tắc cộng, ta có : 60+24+120+48=252 cách đi từ A đến G.