Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có \(a = 3 > 0,b = - 4,c = 1\)
\(\Delta ' = {\left( { - 2} \right)^2} - 3.1 = 1 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\). Khi đó:
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( { - \infty ;\frac{1}{3}} \right)\) và \(\left( {1; + \infty } \right)\);
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( {\frac{1}{3};1} \right)\)
b) Ta có \(a = 9 > 0,b = 6,c = 1\)
\(\Delta ' = 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 1 nghiệm \(x = - \frac{1}{3}\). Khi đó:
\(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\backslash \left\{ { - \frac{1}{3}} \right\}\)
c) Ta có \(a = 2 > 0,b = - 3,c = 10\)
\(\Delta = {\left( { - 3} \right)^2} - 4.2.10 = - 71 < 0\)
\( \Rightarrow \)\(f\left( x \right) > 0\forall x \in \mathbb{R}\)
d) Ta có \(a = - 5 < 0,b = 2,c = 3\)
\(\Delta ' = {1^2} - \left( { - 5} \right).3 = 16 > 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 2 nghiệm \(x = \frac{{ - 3}}{5},x = 1\). Khi đó:
\(f\left( x \right) < 0\) với mọi x thuộc các khoảng \(\left( { - \infty ; - \frac{3}{5}} \right)\) và \(\left( {1; + \infty } \right)\);
\(f\left( x \right) > 0\) với mọi x thuộc các khoảng \(\left( { - \frac{3}{5};1} \right)\)
e) Ta có \(a = - 4 < 0,b = 8c = - 4\)
\(\Delta ' = 0\)
\( \Rightarrow \)\(f\left( x \right)\) có 1 nghiệm \(x = 1\). Khi đó:
\(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\backslash \left\{ 1 \right\}\)
g) Ta có \(a = - 3 < 0,b = 3,c = - 1\)
\(\Delta = {3^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = - 3 < 0\)
\( \Rightarrow \)\(f\left( x \right) < 0\forall x \in \mathbb{R}\)

1.
\(f\left(x\right)=\frac{\left(x^2-3x\right)^2-2\left(x^2-3x\right)-8}{x^2-3x}=\frac{\left(x^2-3x-4\right)\left(x^2-3x+2\right)}{x^2-3x}\)
\(f\left(x\right)=\frac{\left(x+1\right)\left(x-1\right)\left(x-2\right)\left(x-4\right)}{x\left(x-3\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{0;3\right\}\)
\(f\left(x\right)=0\Rightarrow x=\left\{-1;1;2;4\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< -1\\0< x< 1\\2< x< 3\\x>4\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}-1< x< 0\\1< x< 2\\3< x< 4\end{matrix}\right.\)
2.
\(f\left(x\right)=\frac{2x-2\left(x+1\right)-x\left(x+1\right)}{2x\left(x+1\right)}=\frac{-x^2-x-2}{2x\left(x+1\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{-1;0\right\}\)
\(f\left(x\right)>0\Rightarrow-1< x< 0\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< -1\\x>0\end{matrix}\right.\)
3.
\(f\left(x\right)=\frac{x^2-4x+3+\left(x-1\right)\left(3-2x\right)}{3-2x}=\frac{-x^2+x}{3-2x}=\frac{x\left(1-x\right)}{3-2x}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\frac{3}{2}\)
\(f\left(x\right)=0\Rightarrow x=\left\{0;1\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}0< x< 1\\x>\frac{3}{2}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< 0\\1< x< \frac{3}{2}\end{matrix}\right.\)
4.
\(f\left(x\right)=\frac{\left(x-1\right)\left(x+1\right)}{\left(x-\sqrt{3}\right)\left(x+\sqrt{3}\right)\left(2-x\right)\left(3x+4\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{\pm\sqrt{3};-\frac{4}{3};2\right\}\)
\(f\left(x\right)=0\Rightarrow x=\pm1\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}-\sqrt{3}< x< -\frac{4}{3}\\-1< x< 1\\\sqrt{3}< x< 2\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< -\sqrt{3}\\-\frac{4}{3}< x< -1\\1< x< \sqrt{3}\\x>2\end{matrix}\right.\)

1.
\(f\left(x\right)=\frac{x-7}{\left(x-4\right)\left(4x-3\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định tại \(x=\left\{\frac{3}{4};4\right\}\)
\(f\left(x\right)=0\Rightarrow x=7\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}\frac{3}{4}< x< 4\\x>7\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}x< \frac{3}{4}\\4< x< 7\end{matrix}\right.\)
2.
\(f\left(x\right)=\frac{11x+3}{-\left(x-\frac{5}{2}\right)^2-\frac{3}{4}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=-\frac{3}{11}\)
\(f\left(x\right)>0\Rightarrow x< -\frac{3}{11}\)
\(f\left(x\right)< 0\Rightarrow x>-\frac{3}{11}\)
3.
\(f\left(x\right)=\frac{3x-2}{\left(x-1\right)\left(x^2-2x-2\right)}\)
Vậy:
\(f\left(x\right)\) ko xác định khi \(x=\left\{1;1\pm\sqrt{3}\right\}\)
\(f\left(x\right)=0\Rightarrow x=\frac{2}{3}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< 1-\sqrt{3}\\\frac{2}{3}< x< 1\\x>1+\sqrt{3}\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow\left[{}\begin{matrix}1-\sqrt{3}< x< \frac{2}{3}\\1< x< 1+\sqrt{3}\end{matrix}\right.\)
4.
\(f\left(x\right)=\frac{\left(x-2\right)\left(x+6\right)}{\sqrt{6}\left(x+\frac{\sqrt{6}}{4}\right)^2+\frac{8\sqrt{2}-3\sqrt{6}}{8}}\)
Vậy:
\(f\left(x\right)=0\Rightarrow x=\left\{-6;2\right\}\)
\(f\left(x\right)>0\Rightarrow\left[{}\begin{matrix}x< -6\\x>2\end{matrix}\right.\)
\(f\left(x\right)< 0\Rightarrow-6< x< 2\)

a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}

a) Ta lập bảng xét dấu
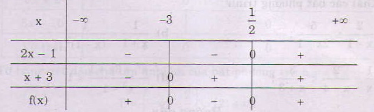
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪

1:
c: =>1/3x+2/3-x+1>x+3
=>-2/3x+5/3-x-3>0
=>-5/3x-4/3>0
=>-5x-4>0
=>x<-4/5
d: =>3/2x+5/2-1<=1/3x+2/3+x
=>3/2x+3/2<=4/3x+2/3
=>1/6x<=2/3-3/2=-5/6
=>x<=-5
2:





