Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Đặt a = B C , b = C A , c = A B .
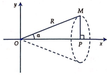
Quay tam giác OCA quanh trung trực của đoạn thẳng CA thì khối tròn xoay sinh ra là khối nón có chiều cao h 1 = R 2 − 1 4 b 2 và bán kính đáy r 1 = 1 2 b nên ta có V 1 = 1 3 π r 1 2 h 1 = 1 24 π b 2 4 R 2 − b 2 .
Tương tự, ta có
V 2 = 1 24 π c 2 4 R 2 − c 2 ; V 3 = 1 24 π a 2 4 R 2 − a 2 .
Bằng việc khảo sát hàm số f t = t 2 4 R 2 − t trên khoảng 0 ; 4 R 2 hoặc dựa vào bất đẳng thức Cô-si
1 2 b 2 . 1 2 b 2 . 4 R 2 − b 2 ≤ 1 2 b 2 + 1 2 b 2 + 4 R 2 − b 2 3 3 = 64 27 R 6 .
Ta được V 1 ≤ 2 π 3 9 R 3 ; V 2 ≤ 2 π 3 9 R 3 . Suy ra V 1 + V 2 ≤ 4 π 3 9 R 3 .
Dấu bằng xảy ra khi và chỉ khi b = c = 2 6 3 R .
Vậy V 1 + V 2 đạt giá trị lớn nhất bằng 4 π 3 9 R 3 khi b = c = 2 6 3 R .
Khi đó tam giác ABC cân tại A và có A B = A C = 2 6 3 R .
Gọi AH là đường cao của tam giác ABC thì 2 R . A H = A B 2 . Từ đó suy ra A H = A B 2 2 R = 4 3 R . Do đó O H = A H − R = 1 3 R và a = 2 R 2 − O H 2 = 4 2 3 R .
Suy ra V 3 = 8 π 81 R 3 .

Đáp án B
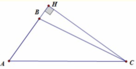
Ta có cos A B C ⏜ = B A 2 + B C 2 - A C 2 2 B A . B C = - 1 2
⇒ A B C ⏜ = 120 ° ⇒ C B H ⏜ = 60 °
Suy ra C H = B C sin 60 ° = 5 3 2
Khi quay tam giác quay AB ta được khối có thể tích là
V = V N 1 - V N 2 = 1 3 πCH 2 . AH - 1 3 πCH 2 . BH
(Trong đó V N 1 ; V N 2 lần lượt là thể tích khối nón tạo thành khi quay các tam giác CBH và CAH quanh AB)
1 3 πCH 2 . AH - BH = 1 3 πCH 2 . AB = 75 4 π t = 2 x > 1 .

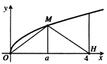
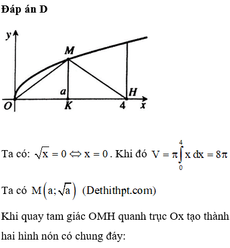
Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.

Đáp án B
Bán kính đường tròn ngoại tiếp tam giác là R = B C 2 sin A = 3 2 sin 60 = 3
Độ dài đường cao là A H = A B sin B 3 3 2
Khi quay quanh đường thẳng AD
Thể tích hình cầu tạo thành là V 1 = 4 3 π R 3 = 4 π 3
Thể tích khối nón tạo thành là V 1 = 1 3 π r 2 h = 1 3 π H B 2 . A H = 23 8 π 3

Giải phương trình:
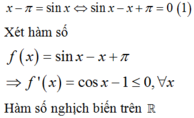
Phương trình (1) có tối đa 1 nghiệm. Mà f π = 0 ⇒ x = π là nghiệm duy nhất của (1).
Thể tích khối tròn xoay tạo thành là:
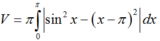
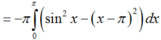
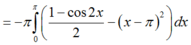

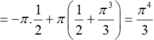
Mà
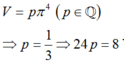
Chọn A.
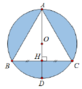

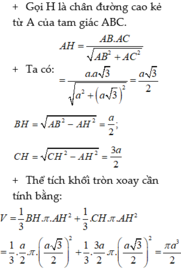
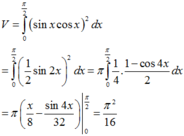

Đáp án B.