Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C K H I
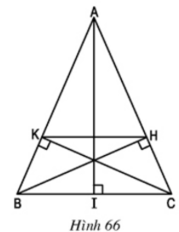
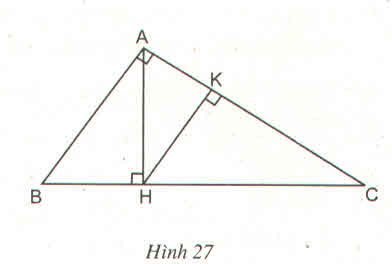
a) Xét hai Δvuông HBC và ΔKCB
∠BCH = ∠CBK (Δ ABC cân tại A) BC cạnh chung
⇒ ΔHBC = ΔKCB (cạnh huyền, góc nhọn)
⇒ CH = BK
b) Ta có: AB = AC (ΔABC cân tại A) và CH = BK
- Quảng cáo -
AK = AB – BK và AH = AC – CH ⇒ AK = AH
⇒ AK/AB = AH/AC ⇒ KH//BC
c) Kẻ đường cao AI của Δ ABC và xét Δ IAC
ΔHBC có ∠ACI = ∠BCH
⇒ ΔIAC ∽ ΔHBC(g.g) ⇒ AC/BC = IC/HC ⇒ HC = IC.BC / AC = a2/2b
Ta có : \(KH//BC\Rightarrow\frac{KH}{BC}=\frac{AH}{AC}\)
\(\Rightarrow KH=\frac{AH.BC}{AC}=\frac{\left(AC-HC\right).BC}{AC}\)
\(\Rightarrow KH=\left(b-\frac{a^2}{2b}\right)\frac{a}{b}=a-\frac{a^3}{2b^2}\)

a:
| AH | 1 | 2 | 3 | 4 | 5 | 10 | 15 | 20 |
| S | 2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 |
b: 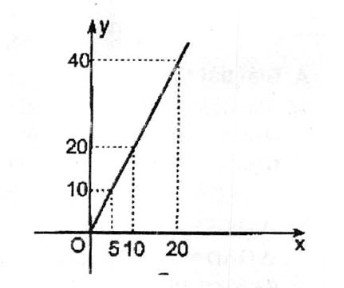
c: Diện tích tam giác tỉ lệ thuận với chiều cao

Em có thể tham khảo tại đây nhé.
Câu hỏi của Nguyễn Tuấn Minh - Toán lớp 8 - Học toán với OnlineMath


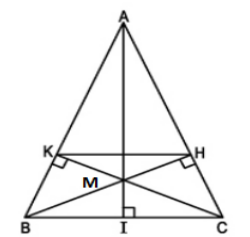
a)
∆ABC có MN // BC.
=> MNCBMNCB = AKAHAKAH(kết quả bài tập 10)
Mà AK = KI = IH
Nên AKAHAKAH = 1313 => MNCBMNCB = 1313 => MN = 1313BC = 1313.15 = 5 cm.
∆ABC có EF // BC => EFBCEFBC = AIAHAIAH = 2323
=> EF = 2323.15 =10 cm.
b) Áp dụng kết quả ở câu b của bài 10 ta có:
SAMN= 1919.SABC= 30 cm2
SAEF= 4949.SABC= 120 cm2
Do đó SMNEF = SAEF - SAMN = 90 cm2
bt 10 là bt nào?
vs lại toàn Áp Dụng bài người khác, ko cm?!

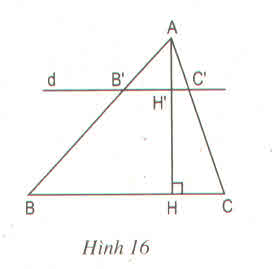
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313
a) Chứng minh AH′AHAH′AH = B′C′BCB′C′BC
Vì B'C' // với BC => B′C′BCB′C′BC = AB′ABAB′AB (1)
Trong ∆ABH có BH' // BH => AH′AHAH′AH = AB′BCAB′BC (2)
Từ 1 và 2 => B′C′BCB′C′BC = AH′AHAH′AH
b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.
Áp dụng kết quả câu a) ta có: AH' = 1313 AH
B′C′BCB′C′BC = AH′AHAH′AH = 1313 => B'C' = 1313 BC
=> SAB’C’= 1212 AH'.B'C' = 1212.1313AH.1313BC
=>SAB’C’= (1212AH.BC)1919
mà SABC= 1212AH.BC = 67,5 cm2
Vậy SAB’C’= 1919.67,5= 7,5 cm2

B C A D E F H Bài làm:
1) Tam giác BDH ~ Tam giác BEC (g.g) vì:
\(\hept{\begin{cases}\widehat{HBD}=\widehat{EBC}\left(gt\right)\\\widehat{BDH}=\widehat{BEC}=90^0\end{cases}}\)
2)
a) Theo phần 1 có 2 tam giác đồng dạng nên ta có tỉ số sau: \(\frac{BH}{BC}=\frac{BD}{BE}\Leftrightarrow BH.BE=BD.BC\left(1\right)\)
b) Tương tự ta CM được: \(CH.CF=CD.BC\left(2\right)\)
Cộng vế (1) và (2) ta được: \(BH.BE+CH.CF=BD.BC+CD.BC\)
\(=\left(BD+DC\right).BC=BC.BC=BC^2\)
3)
a) Tam giác AEB ~ Tam giác AFC (g.g) vì:
\(\hept{\begin{cases}\widehat{BAE}=\widehat{FAC}\left(gt\right)\\\widehat{AEB}=\widehat{CFA}=90^0\end{cases}}\)
\(\Rightarrow\frac{AE}{FA}=\frac{AB}{AC}\)
Tam giác AEF ~ Tam giác ABC (c.g.c) vì:
\(\hept{\begin{cases}\frac{AE}{FA}=\frac{AB}{AC}\left(cmt\right)\\\widehat{FAE}=\widehat{BAC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\)
b) Tương tự a ta CM được: \(\widehat{DEC}=\widehat{ABC}\)
\(\Rightarrow\widehat{AEF}=\widehat{DEC}\Leftrightarrow90^0-\widehat{AEF}=90^0-\widehat{DEC}\Rightarrow\widehat{FEB}=\widehat{BED}\)
=> EB là phân giác của tam giác DEF
Tương tự ta chứng minh được DA,FC là các đường phân giác còn lại của tam giác DEF, mà giao 3 đường này là H
=> H là giao 3 đường phân giác của tam giác DEF
=> H cách đều 3 cạnh của tam giác DEF (tính chất đường pg của tam giác)
4) ch nghĩ ra nhé
4)
+) Gọi I là giao điểm của đường trung trực HC và đường trung trực MN
=> IH = IC; IM = IN
Lại có MH = NC ( gt)
=> \(\Delta\)IMH = \(\Delta\)INC => ^MHI = ^NCI mà ^NCI = ^HCI = ^CHI ( vì IH = IC => \(\Delta\)IHC cân )
=> ^MHI = ^CHI hay ^BHI = ^CHI => HI là phân giác ^BHC
=> I là giao điểm của phân giác ^BHC và trung trực HC
=> I cố định
=> Đường trung trực của đoạn MN luôn đi qua một điểm cố định
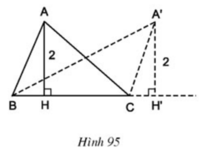

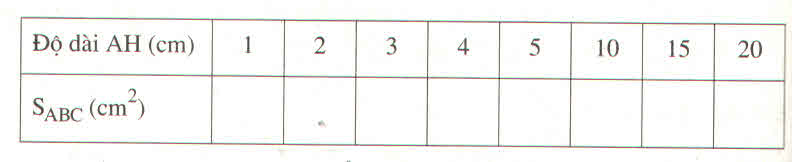



Đỉnh A của các tam giác đó nằm trên đường thẳng song song với BC và cách BC một khoảng bằng 2 cm