Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\left\{{}\begin{matrix}2^x=a\\3^y=b\\4^z=c\end{matrix}\right.\) (với \(a;b;c>0\)) \(\Rightarrow a^2+b^2+c^2=a+b+c\)
\(\Leftrightarrow\left(a-\frac{1}{2}\right)^2+\left(b-\frac{1}{2}\right)^2+\left(c-\frac{1}{2}\right)^2=\frac{3}{4}\)
Gọi \(M\left(a;b;c\right)\) thì M thuộc mặt cầu tâm \(I\left(\frac{1}{2};\frac{1}{2};\frac{1}{2}\right)\) bán kính \(R=\frac{\sqrt{3}}{2}\)
\(T=2^{x+1}+3^{y+1}+4^{z+1}=2.2^x+3.3^y+4.4^z=2a+3b+4c\)
\(\Rightarrow2a+3b+4c-T=0\)
Gọi (P) là mặt phẳng thay đổi có phương trình \(2x+3y+4z-T=0\)
\(\Rightarrow M\in\left(P\right)\Rightarrow M\) thuộc giao của mặt cầu và (P)
Mà mặt cầu giao với (P) khi và chỉ khi:
\(d\left(I;\left(P\right)\right)\le R\Leftrightarrow\frac{\left|2.\frac{1}{2}+3.\frac{1}{2}+4.\frac{1}{2}-T\right|}{\sqrt{2^2+3^2+4^2}}\le\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left|T-\frac{9}{2}\right|\le\frac{\sqrt{87}}{2}\) \(\Rightarrow\frac{-\sqrt{87}}{2}\le T-\frac{9}{2}\le\frac{\sqrt{87}}{2}\)
\(\Rightarrow T\le\frac{9+\sqrt{87}}{2}\)

+ Ta có đạo hàm y’ = x2- 2mx+ (m2-1).
Phương trình y’ =0 có ∆ ' = m 2 - ( m 2 - 1 ) = 1 ⇒ x 1 = m - 1 x 2 = m + 1
+ Không mất tính tổng quát, giả sử A ( x 1 ; y 1 ) , B ( x 2 ; y 2 ) .
A, B nằm khác phía khi và chỉ khi x1. x2< 0 hay ( m-1) (m+ 1) < 0
Suy ra -1< m< 1
A, B cách đều đường thẳng y= 5x-9 suy ra trung điểm I của AB nằm trên đường thẳng đó.
Khi đó ta có:
I ( x 1 + x 2 2 ; y 1 + y 2 2 ) h a y I ( m ; 1 3 m 3 - m )
Ta có:
1 3 m 3 - m = 5 m - 9 ⇔ 1 3 m 3 - 6 m + 9 = 0 ⇔ m 1 = 3 1 3 m 2 + m - 3 = 0
Suy ra m 1 + m 2 + m 3 = 3 + - 1 1 3 = 0 .
Chọn A
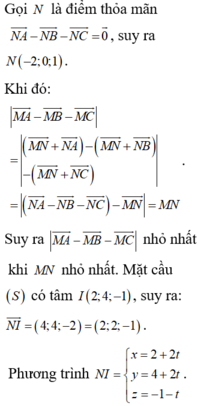


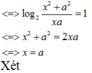
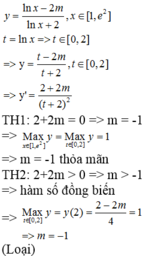
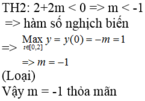

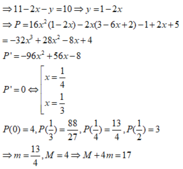
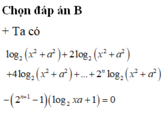


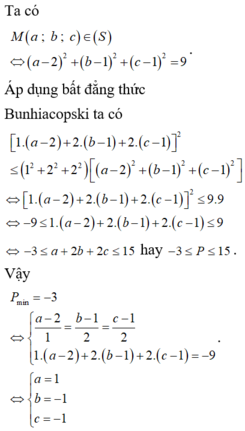

Chọn D.