Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,ĐK:x>0;x\ne9\\ b,A=\dfrac{\sqrt{x}+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ A=\dfrac{2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}=\dfrac{2}{\sqrt{x}+3}\\ c,A>\dfrac{2}{5}\Leftrightarrow\dfrac{2}{\sqrt{x}+3}-\dfrac{2}{5}>0\\ \Leftrightarrow\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{5}>0\\ \Leftrightarrow\dfrac{2-\sqrt{x}}{5\left(\sqrt{x}+3\right)}>0\\ \Leftrightarrow2-\sqrt{x}>0\left(\sqrt{x}+3>0\right)\\ \Leftrightarrow\sqrt{x}< 2\Leftrightarrow0< x< 4\)

a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{x-4}{3\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{3\sqrt{x}}\)
\(=\dfrac{2}{3}\)

a) ĐKXĐ: \(a\ge0;a\ne1\)
\(P=\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left[\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right]\left[\dfrac{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}+a\right)}{1+\sqrt{a}}\right]\)
\(=\left(1+2\sqrt{a}+a\right)\left(1-2\sqrt{a}+a\right)\)
\(=\left(1-a\right)^2\)
b) Để \(P< 7-4\sqrt{3}\)
\(\Rightarrow\left(1-a\right)^2< 7-4\sqrt{3}\)
\(\Leftrightarrow\left|1-a\right|< \left(2-\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{3}-2< a-1< 2-\sqrt{3}\)
\(\Leftrightarrow\sqrt{3}-1< a< 3-\sqrt{3}\)
Vậy \(\sqrt{3}-1< a< 3-\sqrt{3}\) thì \(P< 7-4\sqrt{3}\)

Sửa đề: \(Q=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\right)\)
a) ĐKXĐ: \(\left\{{}\begin{matrix}a\ge0\\a\notin\left\{1;4\right\}\end{matrix}\right.\)
Ta có: \(Q=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a+3\sqrt{a}+2-a+3\sqrt{a}-2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{6\sqrt{a}}\)
\(=\dfrac{a-4}{6a\left(\sqrt{a}-1\right)}\)
c) Thay \(a=9-4\sqrt{5}\) vào Q, ta được:
\(Q=\dfrac{5-4\sqrt{5}}{6\left(9-4\sqrt{5}\right)\left(\sqrt{5}-3\right)}\)
\(=\dfrac{5-4\sqrt{5}}{6\left(9\sqrt{5}-27-20+12\sqrt{5}\right)}\)
\(=\dfrac{5-4\sqrt{5}}{6\left(21\sqrt{5}-47\right)}\)
\(=\dfrac{\left(5-4\sqrt{5}\right)\left(21\sqrt{5}+47\right)}{-24}\)
\(=\dfrac{105\sqrt{5}+235-420-188\sqrt{5}}{-24}\)
\(=\dfrac{-83\sqrt{5}-185}{-24}=\dfrac{83\sqrt{5}+185}{24}\)

`a)P=((1-asqrta)/(1-sqrta)+sqrta).((1+asqrta)/(1+sqrta)-sqrta)`
`=(((1-sqrta)(a+sqrta+1))/(1-sqrta)+sqrta).(((1+sqrta)(a-sqrta+1))/(1+sqrta)-sqrta)`
`=(a+sqrta+1+sqrta)(a-sqrta+1-sqrta)`
`=(a+2sqrta+1)(a-2sqrta+1)`
`=(sqrta+1)^2(sqrta-1)^2`
`=(a-1)^2`
`b)a<7-4sqrt3`
`<=>(a-1)^2<(2-sqrt3)^2`
`<=>sqrt3-2<a-1<2-sqrt3`
`<=>sqrt3-1<a<3-sqrt3`

a) ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne4\end{matrix}\right.\)
b) Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-2}-\dfrac{4}{x-2\sqrt{x}}\right)\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{4}{x-4}\right)\)
\(=\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}-2+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
d) Để A>0 thì \(\sqrt{x}-2>0\)
hay x>4

a) Ta có: \(A=\left(\dfrac{2}{\sqrt{x}-3}+\dfrac{2\sqrt{x}}{x-4\sqrt{x}+3}\right):\dfrac{2\left(x-2\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=\dfrac{2\left(\sqrt{x}-1\right)+2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}:\dfrac{2\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)}\)
\(=\dfrac{4\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{1}{2\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{x}-1}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)^2}\)
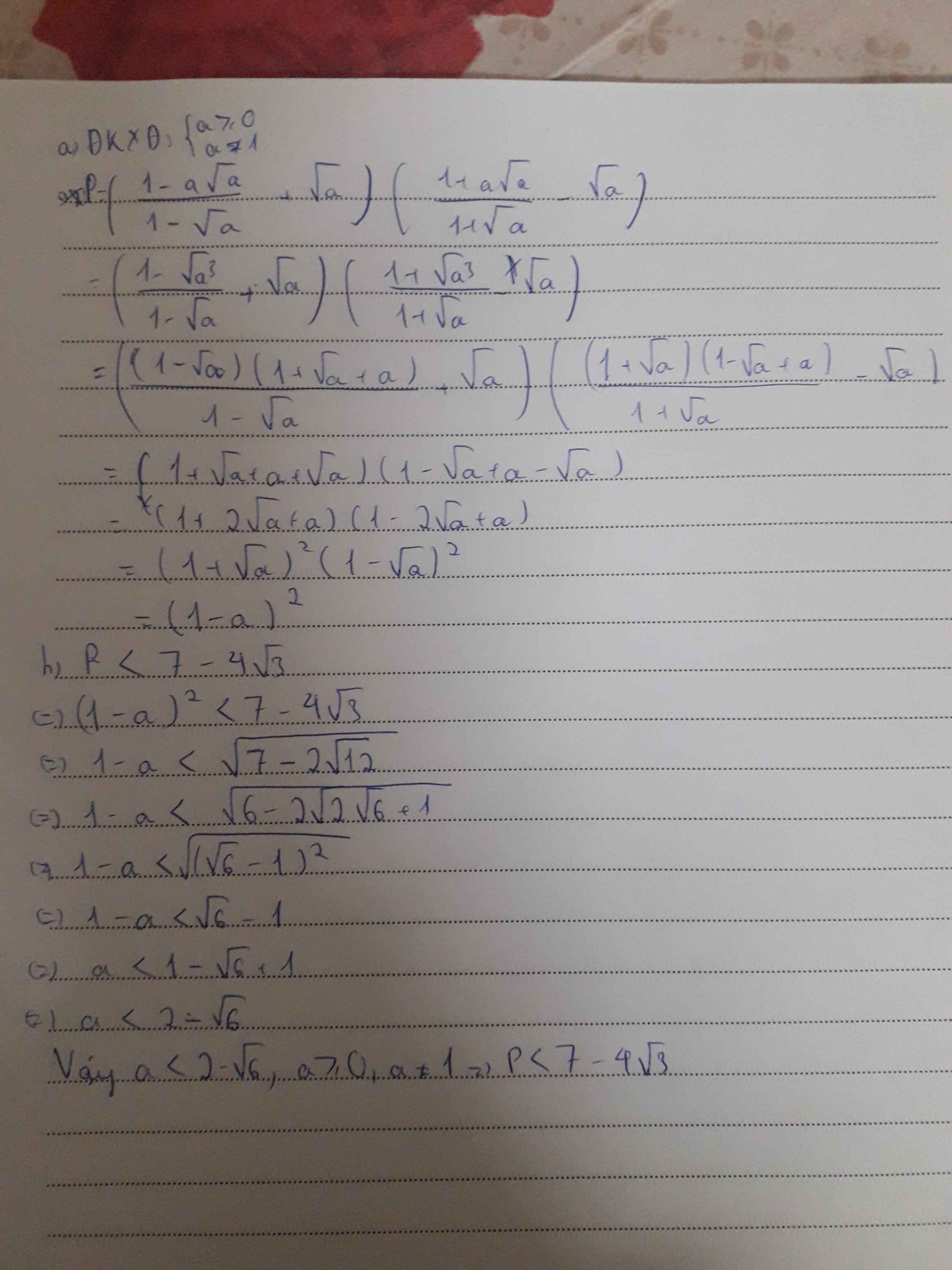
1: \(=\dfrac{3a-12\sqrt{a}+a+4\sqrt{a}-4a-8}{a-16}:\dfrac{\sqrt{a}+4-2\sqrt{a}-5}{\sqrt{a}+4}\)
\(=\dfrac{-8\left(\sqrt{a}+1\right)}{a-16}\cdot\dfrac{\sqrt{a}+4}{-\sqrt{a}-1}=\dfrac{8}{\sqrt{a}-4}\)
2: Để P=-3 thì \(\sqrt{a}-4=-\dfrac{8}{3}\)
=>căn a=4/3
=>a=16/9