Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
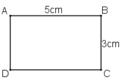
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2)
Hình chữ nhật có kích thước là 1cm x 12cm có diện tích là 12cm2 và chu vi là (1 + 12).2 = 26 (cm) (có 26 > 15)
Hình chữ nhật kích thước 2cm x 7cm có diện tích là 14cm2 và chu vi là (2 + 7).2 = 18 (cm)
(có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
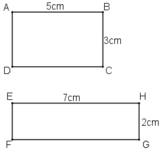
b) + Chu vi hình chữ nhật ABCD đã cho là (5 + 3).2 = 16 cm
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là: 16 : 4 = 4 cm
Diện tích hình vuông này là 4.4 = 16 cm2
(Ở trên hình là ví dụ hình vuông MNPQ có cạnh là 4cm)
Vậy SHCN < SHV
+ Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.
Gọi cạnh của hình chữ nhật có độ dài lần lượt là a, b.
Hình vuông có cùng chu vi với hình chữ nhật nên cạnh hình vuông là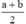 
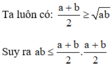
⇒ Hình vuông có diện tích lớn nhất.
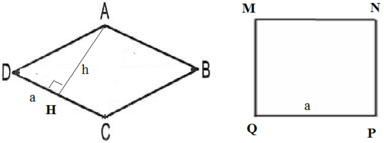
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài a
Ta có: SMNPQ = a2
Từ đỉnh góc từ A của hình thoi ABCD, vẽ đường cao AH có độ dài là h.
ABCD là hình thoi
⇒ ABCD là hình bình hành
⇒ SABCD = ah
Mà ta luôn có h ≤ a (đường vuông góc nhỏ hơn đường xiên)
⇒ ah ≤ a2 ⇒ SABCD ≤ SMNPQ
Vậy diện tích hình vuông luôn lớn hơn diện tích hình thoi.
đặt 2 cạnh hình chữ nhật là (a+k) và (a-k) ta có (a+k).(a-k)= a^2-k^2
để max thì k^2 min => k^2=0 => là hình vuông
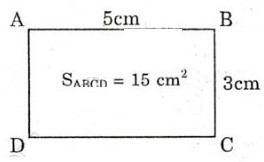
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
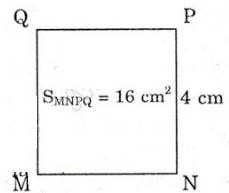
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có 
≥ √ab
Suy ra ab ≤ .
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh .
Trên hình a= 5cm, b = 3cm, = 4cm
a - = 1cm, - b = 1cm
Do đó
SEBCG = b. ( a- ) = 3.1 = 3 (cm2).
SDGHI = . ( - b ) = 4.1 = 4 (cm2).
SAEGD = b. = 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a - , cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng - b, cạnh kia bằng .
Mà a - bằng - b và b < ( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
Hướng dẫn giải:
a) Hình chữ nhật ABCD đã cho có diện tích là SACBD = 3.5 = 15 (cm2).
- Hình chữ nhật có kích thước 1cm x 12cm có diện tích là 12cm2 và chu vi là ( 1+12).2 = 26(cm) (có 26>15).
- Hình chữ nhật có kích thước 2cmx7cm co diện tích là 14cm2 và chu vi là (2+7).2 = 18(cm) (có 18 > 15).
Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD cho trước.
b) Chu vi hình chữ nhật ABCD đã cho là:
(5+3).2 = 16 (cm)
Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:
16:4 = 4(cm).
Diện tích hình vuông này là 4.4 = 16 (m2)
Vậy Shcn < Shv
Trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tich lớn nhất.
Ta luôn có ≥ √ab
Suy ra ab ≤ .
Hình trên là hình vẽ chứng tỏ hình chữ nhật cạnh a,b (a>b) có diện tích nhỏ hơn diện tích hình vuông cạnh .
Trên hình a= 5cm, b = 3cm, = 4cm
a - = 1cm, - b = 1cm
Do đó
SEBCG = b. ( a- ) = 3.1 = 3 (cm2).
SDGHI = . ( - b ) = 4.1 = 4 (cm2).
SAEGD = b. = 3.4 = 12 (cm2).
Nên SABCD = SEBCG + SAEGD = 3 + 12 = 15(cm2).
SAEHI = SDGHI + SAEGD = 4 + 12 = 16 (cm2).
Vậy SABCD < SAEHI
Tổng quát:
Hình chữ nhật EBCG có một cạnh bằng a - , cạnh kia bằng b.
Hình chữ nhật DGHI có một cạnh bằng - b, cạnh kia bằng .
Mà a - bằng - b và b < ( theo giả thiết a> b)
nên SEBCG < SDGHI
Cộng thêm SAEGD vào mỗi vế bất đẳng thức ta được
SEBCG + SAEGD < SDGHI + SAEGD
Vậy SABCD < SAEHI
cách này bản quyền của t nhé :) Cauchy-Schwwarz dạng Engel + Cosi
Ta có :
\(S_{EFGH}=\frac{1}{2}EG^2=\frac{1}{2}\left(EF^2+FG^2\right)=\frac{1}{2}\left(AB^2+BC^2\right)=\frac{1}{2}\left(OA^2+OB^2+OC^2+OD^2\right)\)
\(\ge\frac{1}{2}.\frac{\left(OA+OB+OC+OD\right)^2}{1+1+1+1}=\frac{\left(AC+BD\right)^2}{8}=\frac{AC^2+BD^2+2AC.BD}{8}\)
\(\ge\frac{2\sqrt{\left(AC.BD\right)^2}+2AC.BD}{8}=\frac{2AC.BD+2AC.BD}{8}=\frac{4AC.BD}{8}=\frac{1}{2}AC.BD=S_{ABCD}\)
\(\Rightarrow\)\(S_{EFGH}\ge S_{ABCD}\)
Mà dấu "=" không xảy ra ở cả 2 bđt nên \(S_{EFGH}>S_{ABCD}\)
Vậy hình vuông có diện tích lớn hơn
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a.
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài là a
Ta có: SMNPQ = a2
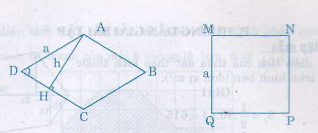
Từ đỉnh góc tù A của hình thoi ABCD vẽ đường cao AH có độ dài h.
Khi đó SABCD = ah
Nhưng h ≤ a (đường vuông góc nhỏ hơn đường xiên) nên ah ≤ a2
Vậy SABCD ≤ SMNPQ
Dấu "=" xảy ra khi h = a hay H trùng với D, nghĩa là hình thoi ABCD trở thành hình vuông.
Với một hình thoi và một hình vuông có cùng chu vi thì hình vuông có diện tích lớn hơn. Vì hai hình này có chu vi bằng nhau nên mỗi cạnh của nó bằng nhau. Giả sử là cạnh có độ dài bằng a.
Diện tích hình vuông là a2
Trong khi hình thoi, ta gọi d1,d2 là độ dài các đường chéo ta có
Diện tích hình thoi là 1/2d1.d2.
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a.
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài là a
Ta có: SMNPQ = a2
Từ đỉnh góc tù A của hình thoi ABCD vẽ đường cao AH có độ dài h.
Khi đó SABCD = ah
Nhưng h ≤ a (đường vuông góc nhỏ hơn đường xiên) nên ah ≤ a2
Vậy SABCD ≤ SMNPQ
Dấu "=" xảy ra khi h = a hay H trùng với D, nghĩa là hình thoi ABCD trở thành hình vuông.
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a.
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài là a
Ta có: SMNPQ = a2
Từ đỉnh góc tù A của hình thoi ABCD vẽ đường cao AH có độ dài h.
Khi đó SABCD = ah
Nhưng h ≤ a (đường vuông góc nhỏ hơn đường xiên) nên ah ≤ a2
Vậy SABCD ≤ SMNPQ
Dấu "=" xảy ra khi h = a hay H trùng với D, nghĩa là hình thoi ABCD trở thành hình vuông.
Gọi a1,a2 lan luot la canh hing vuong 1 va canh hinh vuong 2
P1,P2 ___________ chu vi________________
S1,S2 __________diện tích____________
Theo đề ta có
\(P_1-P_2=12\Leftrightarrow4a_1-4a_2=12\Leftrightarrow a_1-a_2=3\)3
S1-S2=135
\(a_1^2-a_2^2=135\)
\(\Leftrightarrow\left(a_1-a_2\right)\left(a_1+a_2\right)=135\)
\(\Leftrightarrow3\left(a_1+a_2\right)=135\Leftrightarrow a_1+a_2=45\)\(\Leftrightarrow a_1=45-a_2\)
\(a_1-a_2=3\Leftrightarrow45-a_2-a_2=3\Leftrightarrow a_2=\frac{45-3}{2}=21\)
\(\Rightarrow a_1=3+a_2=3+21=24\)
vay canh hv 1 la 24m, cạnh hv 2 la 21 m
hình vuông có chu vi lớn hơn hình tam giác
vì sao