Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

lại lần nữa:
Để mình làm lại :
Số cách xếp bất kỳ 13 học sinh là: \(\left|\Omega\right|=P_{13}\)
Số cách xếp có ít nhất 2 học sinh nữ cạnh nhau là: \(2.P_{12}\)
Số cách xếp không có 2 học sinh nữ cạnh nhau là:
\(P_{13}-2P_{12}=11P_{12}\)
Goi A là biến cố không có 2 học sinh nữ cạnh nhau
\(\Rightarrow\left|A\right|=11.P_{12}\)
\(\Rightarrow P\left(A\right)=\)\(\frac{\left|A\right|}{\left|\Omega\right|}\)\(=\frac{11}{13}\)
Tại sao chỗ xếp ít nhất 2 banj nữ cạnh nhau lại là P12.Nếu đã sắp xếp 2 bạn nữ đứng cạnh nhau rồi thì chỉ còn 11 bạn và sắp xếp theo cách 11! thôi chứ.Là 2!.11!,tại s lại là 2.12!??

Đáp án C
Số cách xếp ngẫu nhiên là 10!.
Ta tìm số cách xếp thoả mãn:
Đánh số hàng từ 1 đến 10. Có hai khả năng:
5 nam xếp vị trí lẻ và 5 nữ xếp vị trí chẵn có 5!x5!= 120 2
5 nam xếp vị trí chẵn và 5 nữ xếp vị trí lẻ có 5!x5!= 120 2
Theo quy tắc cộng có 120 2 + 120 2 =2x 120 2 cách xếp thoả mãn.
Vậy xác suất cần tính 2 ( 5 ! ) 2 10 ! = 1 126

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
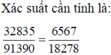

n(omega)=12!
A: "Xếp các học sinh thành 1 hàng ngang sao cho ko có 2 học sinh nữ nào đứng cạnh nhau"
=>\(n\left(A\right)=8!\cdot A^4_9\)
=>P=14/55

+ Xếp 77 nam thành một hàng ngang : 7!7! cách.
+ Có tất cả 88 vị trí có thể xếp các bạn nữ vào (gồm 66 vị trí xen kẽ giữa các bạn nam và 22 vị trí đầu và cuối).
Chọn 44 trong 88 vị trí đó và xếp 44 bạn nữ vào 44 vị trí đã chọn : A48A84 cách.
⇒⇒ số cách xếp thỏa mãn ĐK đề bài là A48.7!=8467200

Đáp án D
Số cách xếp 2 bạn nữ là ![]()
Số cách xếp 2 bạn nữ đứng cạnh nhau là ![]()
Xác suất 2 bạn nữ đứng cạnh nhau là 
Xác suất 2 bạn nữ không đứng cạnh nhau là ![]()

a: Coi 3 bạn nữ như 1 người
Số cách xếp là:
\(8!\cdot3!\)(cách)
b: Số cách xếp là:
\(10!-8!\cdot3!\left(cách\right)\)

Đáp án D
“Xếp 11 học sinh nữa thành 1 hàng dọc” => Số phần tử không gian mẫu n ( Ω ) = 11 !
A:"2 học sinh nữ bất kỳ không xếp cạnh nhau "
Có 7! Cách sắp xếp các học sinh nam thành 1 hàng: 1N2N3N4N5N6N7N8
Khi đó có 8 vị trí xen kẽ các học sinh nam.
Để 2 học sinh nữ bất kỳ không xếp cạnh nhau ta sắp xếp 4 học sinh nữ vào 8 vị trí này có A 8 4 cách sắp xếp.
⇒ n ( A ) = 7 ! . A 8 4 .
Vậy P(A) = 7 ! . A 8 4 11 ! .