Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

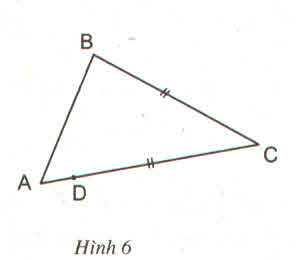
Vì BC = DC.
Mà D nằm giữa A và C nên AC = DA + DC, do đó AC > DC
\( \Rightarrow \)AC > BC
Xét tam giác ABC có AC > BC
\( \Rightarrow \widehat B > \widehat A\) ( trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn)
Vậy khẳng định c là đúng.

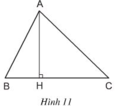
Dựa vào hình vẽ, ta có:
AB, AC là hai đường xiên kẻ từ A đến BC.
HB là hình chiếu của đường xiên AB trên đường thẳng BC.
HC là hình chiếu của đường xiên AC trên đường thẳng BC.
Mà AB < AC nên HB < HC (Đường xiên nào lớn hơn thì có hình chiếu lớn hơn).
Vậy c) đúng.

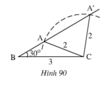
.Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ M, ngày thứ nhất bạn bơi đến A, ngày thứ hai bạn bơi đến B, ngày thứ ba bạn bơi đến C..(hình 12)
Hỏi rằng bạn Nam tập bơi như thế có đúng mục đích đề ra hay không ( ngày hôm sau có bơi xa hơn ngày hôm trước hay không? Vì sao?
Hướng dẫn:
Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D
Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD >AC > AB suy ra
MD > MC >MB > MA
Điều đó có nghĩa là ngày hôm sau bạn Nam bơi đươci xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra

Vì AB < AC (gt) mà AB, AC là hai đường xiên có hai hình chiếu tương ứng là HB và HC nên HB > HC

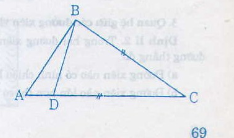
a, Xét △ABI và △ACI có :
AB = AC (gt)
BI = CI (do I là trung điểm BC)
AI chung
=> △ABI = △ACI (c-c-c)
b, Xét △AIC và △DIB có :
AI = DI (gt)
AICˆ=DIBˆAIC^=DIB^ (đối đỉnh)
IC = IB
=> △AIC = △DIB (c-g-c)
=> DBIˆ=ICAˆDBI^=ICA^ (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AC // BD
c, Xét △IKB và △IHC có :
IKBˆ=IHCˆ=90OIKB^=IHC^=90O
IB = IC
KIBˆ=CIHˆKIB^=CIH^ (đối đỉnh)
=> △IKB = △IHC (ch-gn)
=> IK = IH
# mui #
Hắc Long Vương ơi. Bạn chú ý đề bài nha. AB<AC với lại tam giác ABC vuông tại A mà

Góc ABC không phải là góc xen giữa hai cạnh BC và CA góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh - góc - cạnh để kết luận hai tam giác bằng nhau.
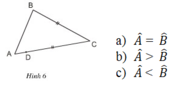

Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.