Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}u_1+u_3=10\\\left(u_1+u_3\right)^2-2u_1u_3=50\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1+u_3=10\\u_1u_3=25\end{matrix}\right.\)
Theo Viet đảo, \(u_1\) và \(u_3\) là nghiệm:
\(x^2-10x+25=0\Rightarrow x=5\)
\(\Rightarrow u_1=u_3=5\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=5\\u_1q^2=5\end{matrix}\right.\) \(\Rightarrow q^2=1\Rightarrow q=\pm1\)

a)
{u6=192u7=384⇔{u1.q5=192(1)u1.q6=384(2){u6=192u7=384⇔{u1.q5=192(1)u1.q6=384(2)
Lấy (2) chia (1): q = 2 thế vào (1):
(1) ⇔ u1.25 = 192 ⇔ u1 = 6
Vậy u1 = 6 và q = 2
b) Ta có:
{u4−u2=72u5−u3=144⇔{u1.q3−u1.q=72u1.q4−u1.q2=144⇔{u1.q(q2−1)=72(1)u1.q2(q2−1)=144(2){u4−u2=72u5−u3=144⇔{u1.q3−u1.q=72u1.q4−u1.q2=144⇔{u1.q(q2−1)=72(1)u1.q2(q2−1)=144(2)
Lấy 2 chia 1: q = 2 thế vào (1)
(1) ⇔2u1(4 – 1) = 72 ⇔ u1 = 12
Vậy u1 = 12 và q = 2
c) Ta có:
{u2+u5−u4=10u3+u6−u5=20⇔{u1.q+u1.q4−u1.q3=10u1.q2(q2−1)=144(2)⇔{u1q(1+q3−q2)=10(1)u1q(1+q3−q2)=20(2){u2+u5−u4=10u3+u6−u5=20⇔{u1.q+u1.q4−u1.q3=10u1.q2(q2−1)=144(2)⇔{u1q(1+q3−q2)=10(1)u1q(1+q3−q2)=20(2)
Lấy (2) chia (1): q = 2 thế vào (1)
(1) ⇔ 2u1 (1 + 8 – 4) = 10 ⇔ u1 = 1
Vậy u1 = 1 và q = 2

a: \(\left\{{}\begin{matrix}u5-u1=15\\u4-u1=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1\cdot q^4-u1=15\\u1\cdot q^3-u1=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1\left(q^4-1\right)=15\\u1\left(q^3-1\right)=6\end{matrix}\right.\Leftrightarrow\dfrac{q^4-1}{q^3-1}=\dfrac{5}{2}\)
=>\(2\left(q^4-1\right)=5\left(q^3-1\right)\)
=>\(2q^4-2-5q^3+5=0\)
=>\(2q^4-5q^3+3=0\)
=>\(2q^4-2q^3-3q^3+3=0\)
=>\(2q^3\left(q-1\right)-3\left(q-1\right)\left(q^2+q+1\right)=0\)
=>\(\left(q-1\right)\left(2q^3-3q^2-3q-3\right)=0\)
=>\(\left[{}\begin{matrix}q=1\\q\simeq2,39\end{matrix}\right.\)
=>\(u1=\dfrac{6}{q^3-1}\simeq\dfrac{6}{2.39^3-1}\simeq0,47\)
b: \(\left\{{}\begin{matrix}u1-u3+u5=65\\u1+u7=325\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1-u1\cdot q^2+u1\cdot q^4=65\\u1+u1\cdot q^6=325\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u1\cdot\left(1-q^2+q^4\right)=65\\u1\left(1+q^6\right)=325\end{matrix}\right.\)
=>\(\dfrac{1-q^2+q^4}{1+q^6}=\dfrac{65}{325}=\dfrac{1}{5}\)
=>\(\dfrac{1}{q^2+1}=\dfrac{1}{5}\)
=>\(q^2+1=5\)
=>q^2=4
=>q=2 hoặc q=-2
TH1: q=2
=>\(u1=\dfrac{325}{q^6+1}=5\)
TH2: q=-2
=>\(u1=\dfrac{325}{\left(-2\right)^6+1}=5\)

Gọi số hạng đầu và công bội của cấp số nhân là: \(u_1;q\).
a) Theo tính chất của cấp số nhân ta có:
\(\left\{{}\begin{matrix}u_1q^4-u_1=15\\u_1q^3-u_1q=6\end{matrix}\right.\)\(\Rightarrow\dfrac{u_1\left(q^4-1\right)}{u_1\left(q^3-q\right)}=\dfrac{15}{6}\)\(\Leftrightarrow\dfrac{\left(q^2-1\right)\left(q^2+1\right)}{q\left(q^2-1\right)}=\dfrac{15}{6}\)\(\Leftrightarrow\dfrac{q^2+1}{q}=\dfrac{15}{6}\)
\(\Leftrightarrow6\left(q^2+1\right)=15q\)\(\Leftrightarrow6q^2-15q+6=0\)\(\Leftrightarrow\left[{}\begin{matrix}q=2\\q=\dfrac{1}{2}\end{matrix}\right.\).
Với \(q=2\).
Suy ra: \(u_1\left(q^4-q\right)=15\Rightarrow u_1=\dfrac{15}{q^4-q}=\dfrac{15}{14}\).
Với \(q=\dfrac{1}{2}\)
Suy ra \(u_1=\dfrac{15}{q^4-q}=\dfrac{-240}{7}\).

Gọi số hạng đầu và công sai của cấp số cộng lần lượt là: u1 và d.
Ta có:
{u1+2u5=0S4=14⇔{u1+2.(u1+4d)=0[2u1+3d].42=14⇔{3u1+8d=02u1+3d=7⇔{u1=8d=−3.
b) Gọi số hạng đầu và công sai của cấp số cộng làn lượt là \(u_1\) d. Ta có:
\(\left\{{}\begin{matrix}u_1+3d=10\\u_1+6d=19\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\).
c) Gọi số hạng đầu và công sai của cấp số cộng lần lượt là \(u_1\) và d. Ta có:
\(\left\{{}\begin{matrix}u_1+u_1+4d-u_1-2d=10\\u_1+u_1+5d=7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+2d=10\\2u_1+5d=7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1=36\\d=-13\end{matrix}\right.\).
d) Gọi số hạng đầu và công sai của cấp số cộng lần lượt là \(u_1\) và d. Ta có:
\(\left\{{}\begin{matrix}u_1+6d-\left(u_1+2d\right)=8\\\left(u_1+d\right)\left(u_1+6d\right)=75\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4d=8\\\left(u_1+d\right)\left(u_1+6d\right)=75\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}d=2\\\left(u_1+2\right)\left(u_1+12\right)=75\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}d=2\\u^2_1+14u_1-51=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}d=\\\left[{}\begin{matrix}u_1=3\\u_1=-17\end{matrix}\right.\end{matrix}\right.\)
Vậy có hai cấp số cộng thỏa mãn là: \(\left\{{}\begin{matrix}d=2\\u_1=3\end{matrix}\right.\) và \(\left\{{}\begin{matrix}d=2\\u_1=-17\end{matrix}\right.\).
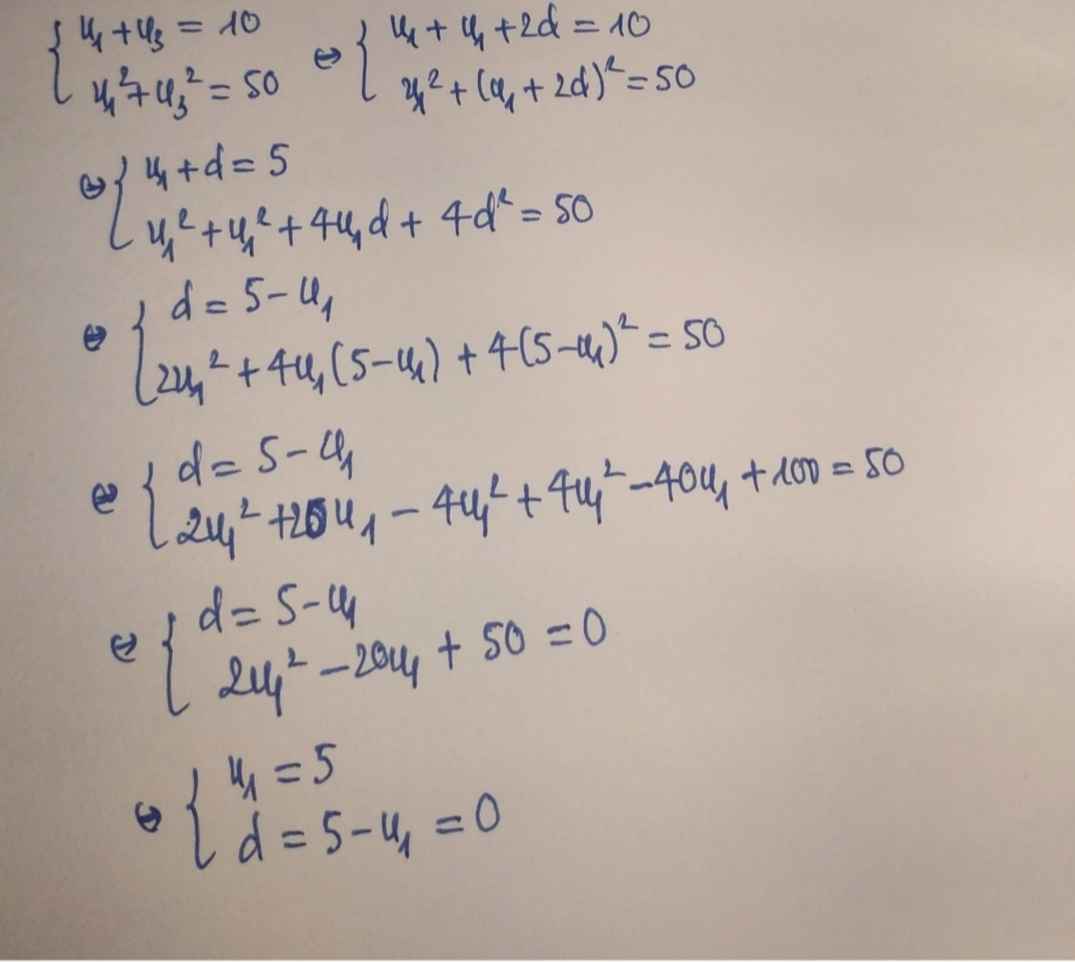
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\\left(u_1+u_3\right)^2-2u_1u_3=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1+u_3=3\\u_1u_3=2\end{matrix}\right.\)
Theo Viet đảo, \(u_1\) và \(u_3\) là nghiệm: \(t^2-3t+2=0\Rightarrow\left[{}\begin{matrix}t=1\\t=2\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}u_1=1\\u_3=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\u_1.q^2=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\q=\pm\sqrt{2}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}u_1=2\\u_3=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=2\\u_1q^2=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=2\\q=\pm\frac{1}{\sqrt{2}}\end{matrix}\right.\)