Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(cosx=t\in\left[-1;1\right]\)
\(\Rightarrow6t^2+\left(9m-7\right)t-6m+2=0\)
\(\Leftrightarrow6t^2-7t+2+9mt-6m=0\)
\(\Leftrightarrow\left(2t-1\right)\left(3t-2\right)+3m\left(3t-2\right)=0\)
\(\Leftrightarrow\left(3t-2\right)\left(2t+3m-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{2}{3}\\cosx=\dfrac{-3m+1}{2}\end{matrix}\right.\)
(Chà tới đây mới thấy ko cần đặt ẩn phụ, nhìn con số 9m và 6m to 1 cách vô lý đã nghi nghi có gì đó bất thường trong nghiệm :D)
Pt \(cosx=\dfrac{2}{3}\) cho 1 nghiệm thuộc \(\left(0;\dfrac{\pi}{2}\right)\)
Để pt có 3 nghiệm pb thì \(cosx=\dfrac{-3m+1}{2}\) cho 2 nghiệm pb thuộc khoảng đã cho
Từ đường tròn lượng giác ta dễ dàng suy ra: \(-1< \dfrac{-2m+1}{2}< 0\)

a) Vẽ đồ thị:
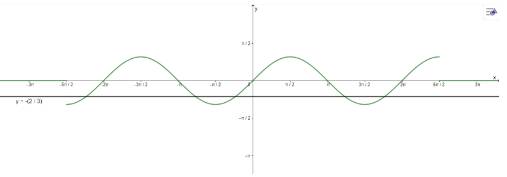
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:

\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm

1.
Từ đường tròn lượng giác ta thấy pt đã cho có nghiệm duy nhất thuộc \(\left[-\frac{\pi}{2};\frac{\pi}{3}\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}2m=1\\0\le2m< \frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m=\frac{1}{2}\\0\le m< \frac{1}{4}\end{matrix}\right.\)
2.
\(\Leftrightarrow3x-\frac{\pi}{3}=x+\frac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=\frac{7\pi}{24}+\frac{k\pi}{2}\)
\(-\pi< \frac{7\pi}{24}+\frac{k\pi}{2}< \pi\Rightarrow-\frac{31}{12}< k< \frac{17}{12}\)
\(\Rightarrow k=\left\{-2;-1;0;1\right\}\) có 4 nghiệm
3.
\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\2x+\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k\pi\\x=\frac{\pi}{4}+k\pi\end{matrix}\right.\) có 4 điểm biểu diễn