Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\left(ax+1\right)\left(ax+b\right)=a^2x^2+x\left(ab+a\right)+b=x^2+7\)
\(\Rightarrow\hept{\begin{cases}a^2=1\\ab+a=0\\b=7\end{cases}}\)
Không tồn tại a, b thỏa mãn
b/ \(\left(ax+b\right)\left(x^2+cx+1\right)=ax^3+x^2\left(ac+b\right)+x\left(a+bc\right)+b=x^3-3x+2\)
\(\Rightarrow\)a = 1 và ac + b = 0 và a + bc = -3 và b = 2
\(\Rightarrow\left(a;b;c\right)=\left(1;2;-2\right)\)


a: \(\Leftrightarrow2x^2+8x+\left(a-8\right)x+4\left(a-8\right)-4a+28⋮x+4\)
hay a=7

a) (2x - 5)(3x + b) = ax^2 + x + c
<=> 6x^2 + 2bx -15x -5b = ax^2 + x + c
<=> -ax^2 + 2bx -5b -c = -6x^2 +16x
Đồng nhất hệ số ta có :
+) -a = -6 => a= 6
+) 2b = 16 => b= 8
+) -5b -c= 0 => c= -40
c ) (ax+b)( x^2 -x-1)= ax^3 - cx^2 - 1
<=> ax^3 -ax^2-ax +bx^2-bx-b= ax^3 - cx^2 - 1
<=> (c+b-a)x^2 -(a+b)x -b = -1
Đồng nhất hệ số ta được:
+) c+b-a =0
+) -a-b = 0
+) -b = -1 => b= 1
Thay b=1 ta được a = -1 và c= -2
<p>a) (2x - 5)(3x + b) = ax^2 + x + c<br><=> 6x^2 + 2bx -15x -5b = ax^2 + x + c<br><=> -ax^2 + 2bx -5b -c = -6x^2 +16x<br>Đồng nhất hệ số ta có :<br>+) -a = -6 => a= 6<br>+) 2b = 16 => b= 8<br>+) -5b -c= 0 => c= -40</p>

\(a,4x^3+ax+b⋮x-2\\ \Leftrightarrow4x^3+ax+b=\left(x-2\right)\cdot a\left(x\right)\)
Thay \(x=2\Leftrightarrow32+2a+b=0\Leftrightarrow2a+b=-32\left(1\right)\)
\(4x^3+ax+b⋮x+1\\ \Leftrightarrow4x^3+ax+b=\left(x+1\right)\cdot b\left(x\right)\)
Thay \(x=-1\Leftrightarrow-4-a+b=0\Leftrightarrow a-b=-4\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\) ta có hệ \(\left\{{}\begin{matrix}2a+b=-32\\a-b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a=-36\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-12\\b=-8\end{matrix}\right.\)

Ta có T = ( a x + 4 ) ( x 2 + b x – 1 )
= a x . x 2 + a x . b x + a x . ( - 1 ) + 4 . x 2 + 4 . b x + 4 . ( - 1 ) = a x 3 + a b x 2 – a x + 4 x 2 + 4 b x – 4 = a x 3 + ( a b x 2 + 4 x 2 ) + ( 4 b x – a x ) – 4 = a x 3 + ( a b + 4 ) x 2 + ( 4 b – a ) x – 4
Theo bài ra ta có
( a x + 4 ) ( x 2 + b x – 1 ) = 9 x 3 + 58 x 2 + 15 x + c đúng với mọi x
ó a x 3 + ( a b + 4 ) x 2 + ( 4 b – a ) x – 4 = 9 x 3 + 58 x 2 + 15 x + c đúng với mọi x.
ó a = 9 a b + 4 = 58 4 b - a = 15 - 4 = c ó a = 9 9 . b = 54 4 b - a = 15 c = - 4 ó a = 9 b = 6 c = - 4
Vậy a = 9, b = 6, c = -4
Đáp án cần chọn là: B
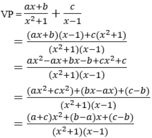
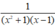 ta được
ta được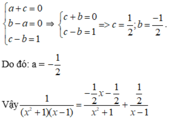
a: \(\left(ax+1\right)\left(ax+b\right)=x^2+7\)
\(\Leftrightarrow a^2x^2+abx+ax+b=x^2+7\)
\(\Leftrightarrow a^2x^2+ax\left(b+1\right)+b=x^2+7\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2=1\\b=7\\a\left(b+1\right)=0\end{matrix}\right.\Leftrightarrow\left(a,b\right)\in\varnothing\)
b: \(\Leftrightarrow ax^3+acx^2+ax+x^2b+cxb+b=x^3-3x+2\)
\(\Leftrightarrow ax^3+x^2\left(ac+b\right)+x\left(a+bc\right)+b=x^3-3x+2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\ac+b=0\\a+bc=3\\b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\\c+2=0\\1+2\cdot\left(-2\right)=3\end{matrix}\right.\Leftrightarrow\left(a,b,c\right)\in\varnothing\)