Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77

Chọn C
- Do công sai và số hạng đầu là d = 1, u 1 = 1 nên đây là tổng của n số tự nhiên đầu tiên là:
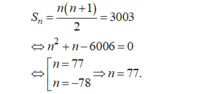

Chọn B
Ta có: S n = 3 n 2 + 4 n = n ( 7 + 6 n + 1 ) 2
⇒ u n = 6 n + 1 ⇒ u 10 = 61

\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d=n\left(n.\dfrac{d}{2}+u_1-\dfrac{d}{2}\right)=n\left(n+4\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{d}{2}=1\\u_1-\dfrac{d}{2}=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=5\\d=1\end{matrix}\right.\)
\(u_n=5+1.\left(n-1\right)=n+4\)

Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4

a) \({u_2} = {u_1} + d\)
\({u_3} = {u_1} + 2d\)
…
\({u_{n - 1}} = {u_1} + \left( {n - 2} \right)d\)
\({u_n} = {u_1} + \left( {n - 1} \right)d\)
\({S_n} = {u_1} + {u_1} + 2d + \ldots + {u_1} + \left( {n - 2} \right)d + {u_1} + \left( {n - 1} \right)d\)
b) \({S_n} = {u_n} + {u_{n - 1}} + \ldots + {u_2} + {u_1} = {u_1} + \left( {n - 1} \right)d + {u_1} + \left( {n - 2} \right)d + \ldots + {u_1} + d + {u_1}\)
c) \(2{S_n} = \left( {{u_1} + {u_1} + d + \ldots + {u_1} + \left( {n - 1} \right)d} \right) + \left( {{u_1} + \left( {n - 1} \right)d + {u_1} + \left( {n - 2} \right)d + \ldots + {u_1}} \right)\).
\( \Rightarrow 2{S_n} = n.\left( {2{u_1} + \left( {n - 1} \right)d} \right)\)
\( \Rightarrow {S_n} = \frac{n}{2}\left( {2{u_1} + \left( {n - 1} \right)d} \right)\)
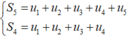
Để xác định cấp số cộng thỏa mãn điều kiện trên, ta cần sử dụng công thức tổng của cấp số cộng.
Công thức tổng của cấp số cộng là: Sn = (n/2)(a1 + an), trong đó Sn là tổng n số hạng đầu, n là số lượng số hạng, a1 là số hạng đầu tiên và an là số hạng cuối cùng.
Theo yêu cầu của bài toán, tổng n số hạng đầu bằng n+1 lần một nửa số hạng thứ n. Ta có thể viết công thức như sau:
Sn = (n/2)(a1 + an) = (n+1)(an/2)
Giải phương trình trên, ta có:
(n/2)(a1 + an) = (n+1)(an/2)
n(a1 + an) = (n+1)an
n(a1 + an) = nan + an
n(a1 - an) = an
Vì n không bằng 0, ta có a1 - an = 1.
Điều này có nghĩa là hiệu giữa số hạng đầu tiên và số hạng cuối cùng của cấp số cộng là 1.
Ví dụ, nếu số hạng đầu tiên là 1, thì số hạng cuối cùng sẽ là 0. Nếu số hạng đầu tiên là 2, thì số hạng cuối cùng sẽ là 1, và cứ tiếp tục như vậy.
Vậy, cấp số cộng thỏa mãn điều kiện là a1 - an = 1, trong đó a1 là số hạng đầu tiên và an là số hạng cuối cùng.