Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(-3;5\right)\cap\left(2;4\right)=\left(-3;5\right)\)
\((-\infty;3]\cap\left[3;5\right]=(-\infty;5]\)
\(\left(-4;2\right)\cap[2;5)=\left(-4;5\right)\)

Tham khảo:
a) Ta có:
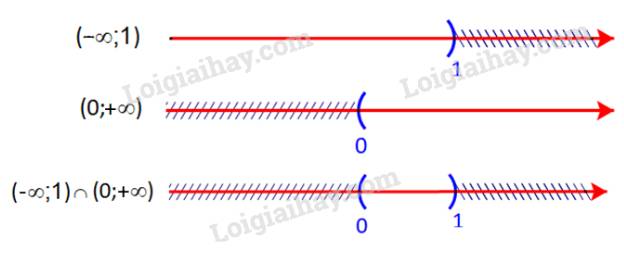
Giao của hai tập hợp là \(( - \infty ;1) \cap (0; + \infty ) = (0;1)\)
b) Ta có:

Hợp của hai tập hợp là \((4;7] \cup ( - 1;5) = ( - 1;7]\)
c) Ta có:
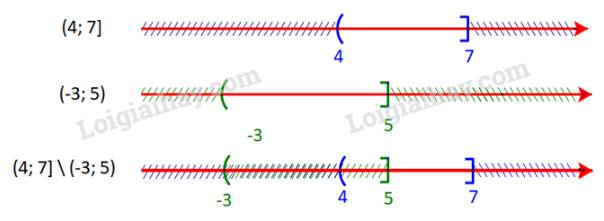
Hiệu của tập hợp \((4;7]\) và tập hợp \(( - 3;5]\) là \((4;7]\;{\rm{\backslash }}\;( - 3;5] = (5;7]\)

\(\left(-\infty;\dfrac{1}{3}\right)\cap\left(\dfrac{1}{4};+\infty\right)=\left(\dfrac{1}{4};\dfrac{1}{3}\right)\)
\(\left(-\dfrac{11}{2};7\right)\cap\left(-2;\dfrac{27}{2}\right)=\left(-2;7\right)\)
\(\left(0;12\right)\cap[5;+\infty)=[5;12)\)
\(R\cap\left[-1;1\right]=\left[-1;1\right]\)

a) (\(-2;3\)]
b) \(\left(-15;14\right)\)
c) \(\left(0;5\right)\)
d) (\(-\infty;4\)] \(\cup\) [\(1;+\infty\))

Tham khảo:
a) Ta có:

Giao của hai tập hợp là \(( - 4;1] \cap [0;3) = \left[ {0;1} \right]\)
b) Ta có:
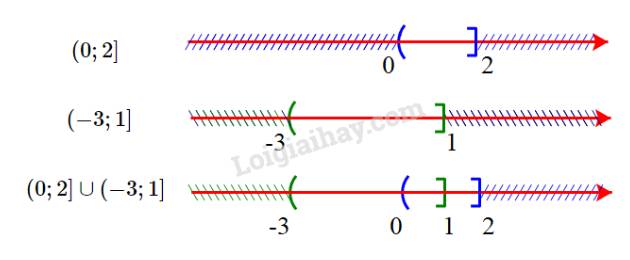
Hợp của hai tập hợp là \((0;2] \cup ( - 3;1] = ( - 3;2]\)
c) Ta có:
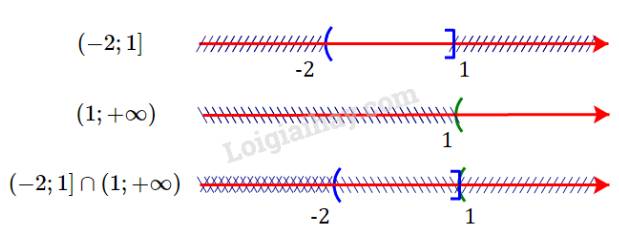
Giao của hai tập hợp là \(( - 2;1] \cap (1;+ \infty )= \emptyset\)
d) Ta có:

Phần bù của tập hợp \(( - \infty ;3]\) trong \(\mathbb{R}\) là \(\mathbb{R}{\rm{\backslash }}( - \infty ;3] = (3; + \infty )\)

a) (\(-\infty;0\)] \(\cup\left[1;2\right]\cup\) [\(3;+\infty\))
b) (\(-\infty;4\)] \(\cup\) [\(5;+\infty\))
c) \(\left(-2;1\right)\cup\left(3;7\right)\)
d) (\(-1;1\)] \(\cup\) [\(4;5\))
a) (-12; 3] ∩ [-1; 4] = [-1; 3]
b) (4, 7) ∩ (-7; -4) = Ø
c) (2; 3) ∩ [3; 5) = Ø
d) (-∞; 2] ∩ [-2; +∞)= [-2; 2].