Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{5x}{10}=\dfrac{x}{2}\)
b) \(\dfrac{4xy}{2y}=2x\left(y\ne0\right)\)
c) \(\dfrac{5x-5y}{3x-3y}=\dfrac{5}{3}\left(x\ne y\right)\)
d) \(\dfrac{x^2-y^2}{x+y}=x-y\left(đk:x\ne-y\right)\)
e) \(\dfrac{x^3-x^2+x-1}{x^2-1}=\dfrac{x^2+1}{x+1}\left(đk:x\ne\pm1\right)\)
f) \(\dfrac{x^2+4x+4}{2x+4}=\dfrac{x+2}{2}\left(đk:x\ne-2\right)\)

a) Đường thẳng \(y = - 5x - 5\) có hệ số góc là \(a = - 5\).
b) Đường thẳng \(y = \sqrt 3 x + 3\) có hệ số góc là \(a = \sqrt 3 \).
c) Đường thẳng \(y = \sqrt {11} x + \sqrt 7 \) có hệ số góc là \(a = \sqrt {11} \).
a, Hệ số góc: -5
b, Hệ số góc: \(\sqrt{3}\)
c, Hệ số góc: \(\sqrt{11}\)

Bài 1:
a: ĐKXĐ: \(x+4\ne0\)
=>\(x\ne-4\)
b: ĐKXĐ: \(2x-1\ne0\)
=>\(2x\ne1\)
=>\(x\ne\dfrac{1}{2}\)
c: ĐKXĐ: \(x\left(y-3\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne0\\y-3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\y\ne3\end{matrix}\right.\)
d: ĐKXĐ: \(x^2-4y^2\ne0\)
=>\(\left(x-2y\right)\left(x+2y\right)\ne0\)
=>\(x\ne\pm2y\)
e: ĐKXĐ: \(\left(5-x\right)\left(y+2\right)\ne0\)
=>\(\left\{{}\begin{matrix}x\ne5\\y\ne-2\end{matrix}\right.\)
Bài 2:
a: \(\dfrac{-12x^3y^2}{-20x^2y^2}=\dfrac{12x^3y^2}{20x^2y^2}=\dfrac{12x^3y^2:4x^2y^2}{20x^2y^2:4x^2y^2}=\dfrac{3x}{5}\)
b: \(\dfrac{x^2+xy-x-y}{x^2-xy-x+y}\)
\(=\dfrac{\left(x^2+xy\right)-\left(x+y\right)}{\left(x^2-xy\right)-\left(x-y\right)}\)
\(=\dfrac{x\left(x+y\right)-\left(x+y\right)}{x\left(x-y\right)-\left(x-y\right)}=\dfrac{\left(x+y\right)\left(x-1\right)}{\left(x-y\right)\left(x-1\right)}\)
\(=\dfrac{x+y}{x-y}\)
c: \(\dfrac{7x^2-7xy}{y^2-x^2}\)
\(=\dfrac{7x\left(x-y\right)}{\left(y-x\right)\left(y+x\right)}\)
\(=\dfrac{-7x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{-7x}{x+y}\)
d: \(\dfrac{7x^2+14x+7}{3x^2+3x}\)
\(=\dfrac{7\left(x^2+2x+1\right)}{3x\left(x+1\right)}\)
\(=\dfrac{7\left(x+1\right)^2}{3x\left(x+1\right)}=\dfrac{7\left(x+1\right)}{3x}\)
e: \(\dfrac{3y-2-3xy+2x}{1-3x-x^3+3x^2}\)
\(=\dfrac{3y-2-x\left(3y-2\right)}{1-3x+3x^2-x^3}\)
\(=\dfrac{\left(3y-2\right)\left(1-x\right)}{\left(1-x\right)^3}=\dfrac{3y-2}{\left(1-x\right)^2}\)
g: \(\dfrac{x^2+7x+12}{x^2+5x+6}\)
\(=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+3\right)\left(x+2\right)}\)
\(=\dfrac{x+4}{x+2}\)

\(a,2\left(x-1\right)\left(x+1\right)+\left(x-1\right)^2+\left(x+1\right)^2\)
\(=2\left(x^2-1\right)+x^2-2x+1+x^2+2x+1\)
\(=2x^2-2+2x^2+2=4x^2\)
\(b,\left(x-y+1\right)^2+\left(1-y\right)^2+2\left(x-y+1\right)\left(y-1\right)\)
\(=\left(x-y+1\right)^2+2\left(x-y+1\right)\left(y-1\right)+\left(y-1\right)^2\)
\(=\left[\left(x-y+1\right)+\left(y-1\right)\right]^2\)
\(=\left[x-y+1+y-1\right]^2=x^2\)
đề cuối phải sửa cái cuối thành \(\left(3x+5\right)^2\)
\(c,\left(3x+1\right)^2-2\left(3x+1\right)\left(3x+5\right)+\left(3x+5\right)^2\)
\(=\left[\left(3x+1\right)-\left(3x+5\right)\right]^2=\left[3x+1-3x-5\right]^2=16\)

(d1): 2x + y - 3 = 0
y = -2x + 2
(d2): y = 5 - 2x
y = -2x + 5
(d3): 2y = x + 4
y = x/2 + 2
(d4): x + y - 1 = 0
y = -x + 1
*) Cặp đường thẳng song song:
(d1) và (d2)
*) Các cặp đường thẳng cắt nhau:
(d1) và (d3); (d1) và (d4); (d2) và (d3); (d2) và (d4); (d3) và (d4)

a) Hàm số \(y = 4x + 2\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = 4;b = 2\).
b) Hàm số \(y = 5 - 3x = - 3x + 5\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = - 3;b = 5\).
c) Hàm số \(y = 2 + {x^2}\) không phải là hàm số bậc nhất vì không có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\).
d) Hàm số \(y = - 0,2x\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = - 0,2;b = 0\).
e) Hàm số \(y = \sqrt 5 x - 1\) là hàm số bậc nhất vì có dạng \(y = ax + b\) với\(a,b\) là các số cho trước và \(a \ne 0\). Ta có, \(a = \sqrt 5 ;b = - 1\).
a) \(y=4x+2\Rightarrow\left\{{}\begin{matrix}a=4\\b=2\end{matrix}\right.\)
b) \(y=5-3x\Rightarrow\left\{{}\begin{matrix}a=-2\\b=5\end{matrix}\right.\)
c) \(y=2+x^2\) không phải hàm số bậc nhất.
d) \(y=0,2x\Rightarrow\left\{{}\begin{matrix}a=-0,2\\b=0\end{matrix}\right.\)
e) \(y=\sqrt[]{5}x-1\Rightarrow\left\{{}\begin{matrix}a=\sqrt[]{5}\\b=-1\end{matrix}\right.\)

a) Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2; - 6} \right);\left( { - 1; - 3} \right);\left( {0;0} \right);\left( {1;3} \right);\left( {2;6} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây
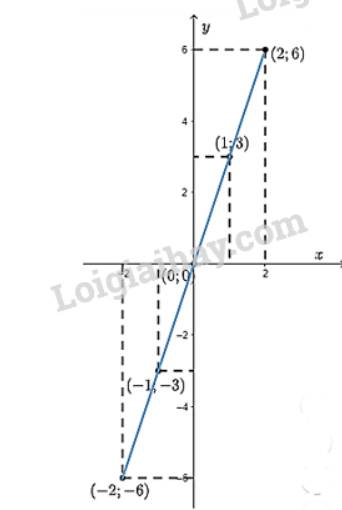
b) Các điểm vừa xác định được ở câu a đều nằm trên một đường thẳng.

Đường thẳng y = 1 – 2x cắt đường thẳng y = 2x + 1 vì – 2 ≠ 2.
Đường thẳng y = 1 – 2x cắt đường thẳng y = 2x vì – 2 ≠ 2.
Đường thẳng y = 1 – 2x cắt đường thẳng y = 2 + 2x vì – 2 ≠ 2.


a: Phương trình hoành độ giao điểm là:
-3x-3=-2x
=>-3x+2x=3
=>-x=3
=>x=-3
Thay x=-3 vào y=-2x, ta được:
\(y=-2\cdot\left(-3\right)=2\cdot3=6\)
Vậy: Hai đường thẳng y=-3-3x và y=-2x cắt nhau tại điểm A(-3;6)
b: Phương trình hoành độ giao điểm là:
\(3\left(x-1\right)-5x=-\sqrt{5}\cdot x-2\)
=>\(-2x-3=-\sqrt{5}\cdot x=-2\)
=>\(-2x+x\cdot\sqrt{5}=-2+3=1\)
=>\(x\left(\sqrt{5}-2\right)=1\)
=>\(x=\dfrac{1}{\sqrt{5}-2}=\sqrt{5}+2\)
Thay \(x=\sqrt{5}+2\) vào y=3(x-1)-5x, ta được:
\(y=3x-3-5x=-2x-3=-2\cdot\left(\sqrt{5}+2\right)-3\)
\(=-2\sqrt{5}-4-3=-2\sqrt{5}-7\)
Vậy: Tọa độ giao điểm của hai đường thẳng \(y=-x\sqrt{5}-2;y=3\left(x-1\right)-5x\) là \(B\left(\sqrt{5}+2;-2\sqrt{5}-7\right)\)