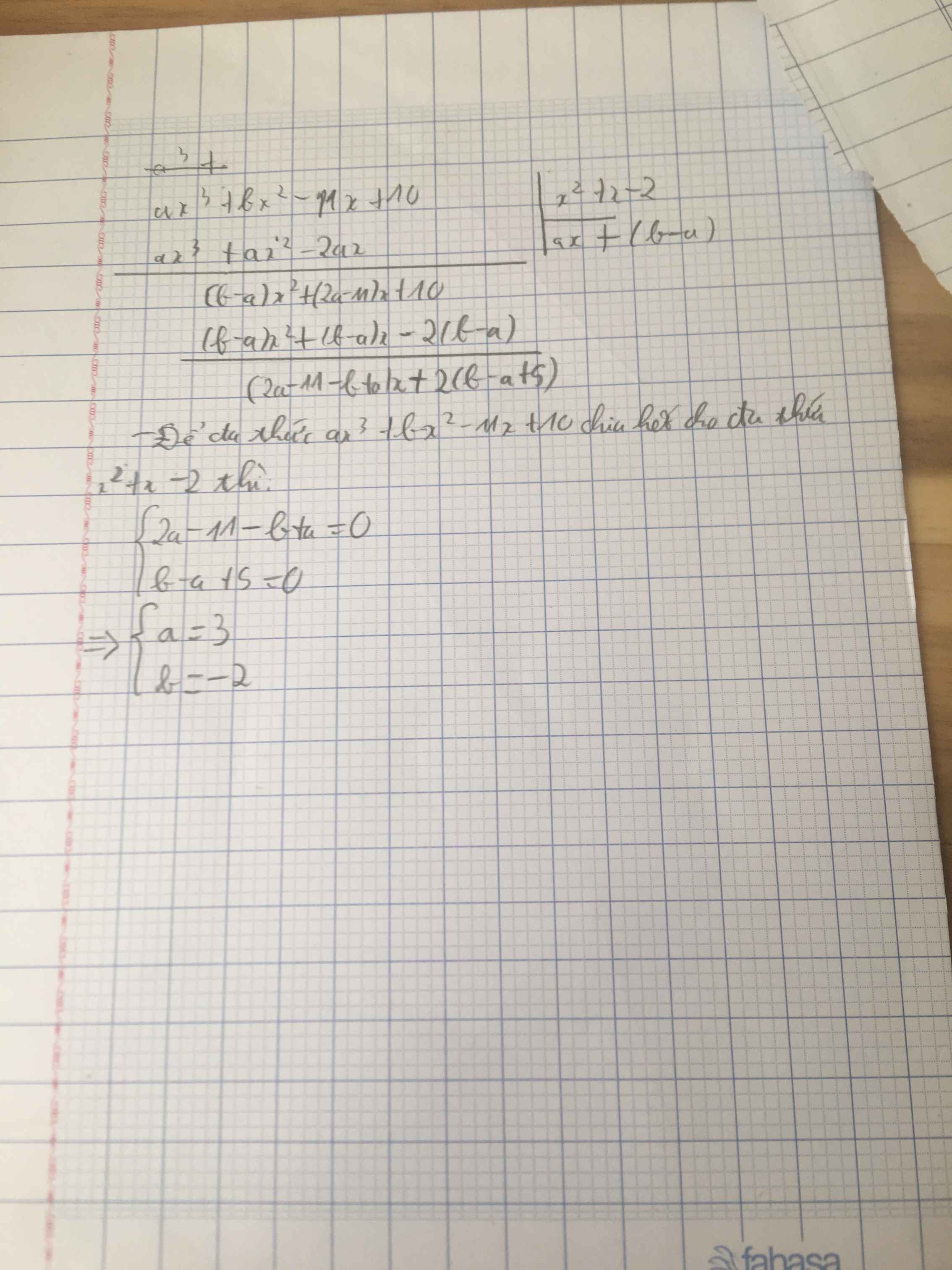SD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SD
0
28 tháng 9 2016
câu 1:
x2y+xy2-x-y
=(x2y-x)+(xy2y)
=x(xy-1)+y(xy-1)
=(x+y)(xy-1)
Câu 2:sai đề
Câu 3:
ax2+ay-bx2-by
=(ax2+ay)-(bx2+by)
=a(x2+y)-b(x2+y)
=(a-b)(x2+y)
Câu 4:
x(x+1)2+x(x-5)-5(x+1)2
=(x+1)2(x-5)+x(x-5)
=(x+5)[(x+1)2+x]
=(x+5)(x2+3x+1)
Câu 5:
3x2-12y2
=3(x2-4y2)
=3[(x)2-(2y)2]
=3(x-2y)(x+2y)
Câu 6:
5xy2-10xyz+5xz2
=5x(y2-2yz+z2)
=5(z-y)2
TN
28 tháng 9 2016
c1 = xy(x+y) - (x+y)
= (x+y)(xy-1)
c2 đề sai
c3 = a(x2+y)-b(x2+y)
= (x2+y)(a-b)
mk làm mẫu cho mấy câu thui nha (mỏi tay quá) hiii. vì đây là toán dạng cơ bản
PT
0
HH
2
AH
Akai Haruma
Giáo viên
30 tháng 1 2022
Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$
$x^2+x-2=(x-1)(x+2)$
Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$
$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức)
$\Leftrightarrow a+b-1=-8a+4b+32=0$
$\Leftrightarrow a=3; b=-2$
MT
21 tháng 8 2015
a) x^3 + x^2 - x - 1
=(x3+x2)+(-x-1)
=x2.(x+1)-(x+1)
=(x+1)(x2-1)
=(x+1)(x-1)(x+1)
=(x+1)2(x-1)
b) a^3 + a^2.b - a^2.c - a.b.c
=(a3+a2b)+(-a2c-abc)
=a2.(a+b)-ab.(a+b)
=(a+b)(a2-ab)
=a.(a+b)(a-b)