Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

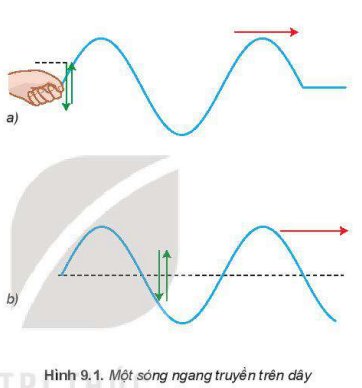
Phương dao động của các phần tử của dây là dao động lên xuống theo phương vuông góc với phương truyền sóng. Phương truyền sóng là phương ngang.

Tham khảo:
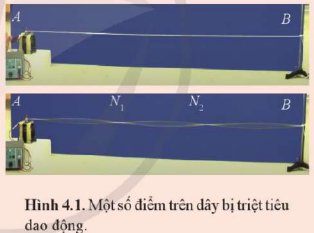
- Những điểm đứng yên này giống với những điểm đứng yên trong hiện tượng giao thoa của sóng nước.
- Tại những điểm dao động tại đó bị triệt tiêu là do sóng tới và sóng phản xạ tại điểm đó ngược pha với nhau.

Xây dựng phương án: Treo quả cầu ở một đầu lò xo, đầu còn lại của lò xo treo lên giá thí nghiệm. Nối một sợi dây với quả cầu. Ban đầu, vật treo trên lò xo đứng yên, lò xo nằm trên trục thẳng đứng. Ta tác dụng một lực kéo nhỏ lên sợi dây theo phương thẳng đứng chiều từ trên xuống dưới.
Thực hiện phương án: Quan sát thấy lò xo dãn rồi co lần lượt, vật chuyển động qua lại quanh vị trí ban đầu (vị trí cân bằng). Như vậy, ta có được dao động của vật treo ở đầu lò xo.

Tính giá trị trung bình: \(\overline A = \frac{{{A_1} + {A_2} + ... + {A_n}}}{n}\)
- Xác định sai số tuyệt đối ứng với mỗi lần đo là trị tuyệt đối của hiệu giữa giá trị trung bình và giá trị của mỗi lần đo
\(\Delta \overline {{A_1}} = \left| {\overline A - \left. {{A_1}} \right|} \right.\)
\(\Delta \overline {{A_2}} = \left| {\overline A - \left. {{A_2}} \right|} \right.\)
…
\(\Delta \overline {{A_n}} = \left| {\overline A - \left. {{A_n}} \right|} \right.\)
- Tính sai số tuyệt đối trung bình của n lần đo gọi là sai số ngẫu nhiên:
\(\overline A = \frac{{\Delta {A_1} + \Delta {A_2} + ... + \Delta {A_n}}}{n}\)
- Sai số tuyệt đối của phép đo là tổng sai số ngẫu nhiên và sai số dụng cụ:
\(\Delta A = \Delta \overline A + \Delta A'\)

a) Chu kì dao động của thuyền: T = \(\frac{{40}}{{24}}\) ≈ 1,7s
b) Tốc độ lan truyền của sóng: v = \(\frac{{10}}{5}\) = 2 (m/s)
c) Bước sóng: λ = \(\frac{v}{f}\) = vT = 2. \(\frac{{40}}{{24}}\) ≈ 3,3m
d) Biên độ sóng: A = 12 cm

Tham khảo:
Nguyên nhân gây ra sai số của phép đo:
+ Sai số dụng cụ đo
+ Thao tác thực hiện không đúng
+ Chưa RESET máy đo thời gian hiện số

tham khảo
1. Mô tả dao động điều hòa của con lắc đơn:
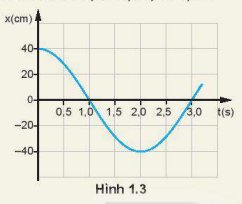
+ Tại thời điểm ban đầu t = 0, con lắc đơn đang ở vị trí biên dương (x = A = 40 cm) và sẽ dịch chuyển về vị trí cân bằng, con lắc đơn ở vị trí x = 0 khi t = 1 s.
+ Tại thời điểm t = 1 s, con lắc đơn bắt đầu chuyển động về phía biên âm và ở vị trí x = - A = - 40 cm khi t = 2 s.
+ Tại thời điểm t = 2 s, con lắc đang ở vị trí biên âm sẽ dịch chuyển về vị trí cân bằng và ở tại vị trí x = 0 khi t = 3 s.
2. Sử dụng thước kẻ để xác định li độ của con lắc tại các thời điểm.
Cách làm: Từ các thời điểm bài toán yêu cầu, dựng đường thẳng vuông góc với trục thời gian tại vị trí thời điểm đó, đường thẳng cắt đồ thị tại điểm nào thì ta kẻ đường thẳng song song với trục thời gian đi qua điểm cắt đó. Đường thẳng song song này cắt trục Ox tại điểm nào thì đó là li độ cần tìm.
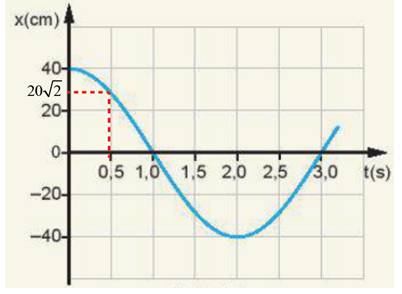
Tại thời điểm t = 0 vật bắt đầu xuất phát nên\(\left\{{}\begin{matrix}A=40cm\\x=40cm\end{matrix}\right.\)
Tại thời điểm t = 0,5 s: \(\left\{{}\begin{matrix}A=40cm\\x=20\sqrt{2}cm\end{matrix}\right.\)
Tại thời điểm t = 2,0 s, con lắc đang ở biên âm\(\left\{{}\begin{matrix}A=40cm\\x=-40cm\end{matrix}\right.\)

a) Biên độ A= 2 mm
Tần số góc ω = 180π (rad/s)
Chu kì \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{180\pi }} = \frac{1}{{90}}s\)
Tần số \(f = \frac{1}{T} = 90Hz\)
b) Phương trình vận tốc là:
v = −180π.2sin(180πt) = 360πsin(180πt) (mm/s)
Phương trình gia tốc là: a = −(180π)2.2cos(180πt) (mm/s2)


Giữ một đầu thước cố định, một đầu tự do (gắn/giữ một đầu thước trên mép bàn). Nhấn đầu thước tự do xuống một biên độ nhỏ quan sát được nhưng không làm thước bị biến dạng, không thể trở lại như ban đầu. Đầu thước sẽ chuyển động lên xuống quanh vị trí ban đầu (vị trí cân bằng), đó có thể xem là dao động tự do của đầu thước.