Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(A=\dfrac{1+x^2+\dfrac{1}{x}}{2+\dfrac{1}{x}}=1\Leftrightarrow\left\{{}\begin{matrix}x\ne0;x\ne-\dfrac{1}{2}\\1+x^2+\dfrac{1}{x}=2+\dfrac{1}{x}\end{matrix}\right.\)
\(\Rightarrow x^2=1\Rightarrow x=\pm1\)


Giá trị biểu thức bằng 0 khi
⇒ x = 0 hoặc (x + 1) = 0 hoặc x – 1 = 0
x + 1 = 0 hay x = - 1
x – 1 = 0 hay x = 1
x = 0 không thỏa mãn điều kiện nên loại
Vậy x = 1 hoặc x = -1

Để B nguyên thì \(x^2-2x+4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Lời giải:
Ta có: $B=\frac{x(x-2)+4}{x-2}=x+\frac{4}{x-2}$
Với $x$ nguyên, để $B$ nguyên thì $\frac{4}{x-2}$ nguyên.
Vì $x-2$ nguyên nên $\frac{4}{x-2}$ nguyên khi mà $x-2$ là ước của $4$
$\Rightarrow x-2\in\left\{\pm 1; \pm 2; \pm 4\right\}$
$\Rightarrow x\in\left\{3; 1; 0; 4; 6; -2\right\}$

1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)

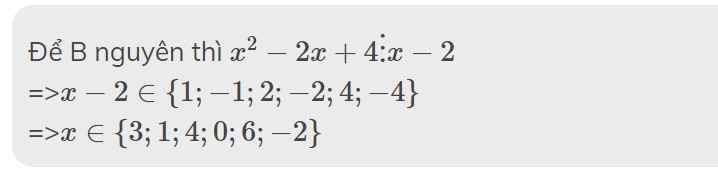
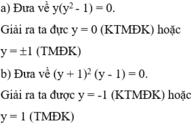

Giá trị biểu thức bằng 0
Khi x 3 + x 2 - x - 1 ⇒ x 2 x + 1 - x + 1 = 0
⇒ x + 1 x 2 - 1 = 0
⇒ x + 1 = 0 hoặc x – 1 = 0
x + 1 = 0 ⇒ x = −1
x - 1 = 0 ⇒ x = 1
x = 1 và x = -1 không thỏa mãn điều kiện
Vậy không có giá trị nào của x để giá trị tương ứng của biểu thức bằng 1