Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Tập xác định: D = ℝ \ 1 2 ⇒ Hàm số y = m x + 1 2 x − 1 liên tục và đơn điệu trên 1 ; 3
⇒ a . b = y 1 . y 3 = m + 1 1 . 3 m + 1 5 = 1 5
⇔ m + 1 3 m + 1 = 1 ⇔ 3 m 2 + 4 m = 0 ⇔ m = 0 m = − 4 3
Vậy có 2 giá trị m thỏa mãn.

Đáp án A
Ta có: y’ = 3 x 2 + 4 m x + m 2
Hàm số đạt cực tiểu tại x = 1
⇒ y’(1) = 0
⇒ m = -3 hoặc m = -1
Với m = -3, ta có:
y’ = 0 ⇔ x = 1 hoặc x = 3
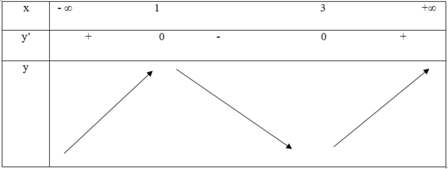
Vậy m = -3 không thoản mãn yêu cầu bài toán
Với m = -1, ta có:
y’ = 0 ⇔ x = 1 hoặc x = 1 3
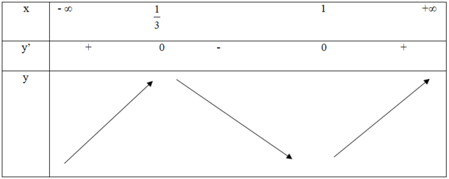
Vậy m = -1 thỏa mãn yêu cầu bài toán


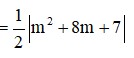
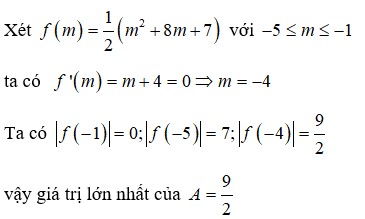

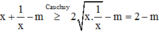

Đáp án A
Ta có y ' = m 2 + 1 x + m 2 > 0 với ∀ x ∈ T X D . Để hàm số đạt giá trị lớn nhất bằng 1 3 trên 0 ; 2 điều kiện cần và đủ là y 2 = 1 3 ⇔ 2 m − 1 2 + m = 1 3 ⇒ m = 1