Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

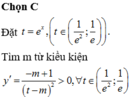

Đáp án C
Ta có: y’ = 3x2 + 2(m+1)x – (3m+2)
Hàm số đồng biến trên khoảng (0;1)
3x2 + 2(m+1)x – (3m+2) ≥ 0 ∀ x ∈ (0;1)
⇔ m ≤ − 3 x 2 + 2 x − 2 2 x − 3 ∀ x ∈ (0;1)
Xét hàm số: g = − 3 x 2 + 2 x − 2 2 x − 3 D =(0;1)
Ta có: g’ = − 6 x 2 − 18 x − 2 ( 2 x − 3 ) 2
ð g’ = 0 ⇔ x = 9 ± 93 6 (không thoản mãn)
Ta có bảng biến thiên
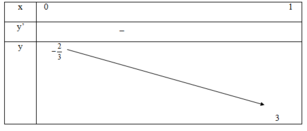
Vậy với m ≤ 3 hàm số đồng biến trên khoảng (0;1)

Đáp án C
Đặt t = e x do x ∈ - 2 ; - 1 ⇒ t ∈ 1 e 2 ; 1 e khi đó y = t - 1 t - m t ≠ m
Ta có y ' = - m + 1 t - m 2 , để hàm số đồng biến - m + 1 > 0 m ∈ 1 e 2 ; 1 e ⇒ [ m ≤ 1 e 2 1 e ≤ m < 1

Đáp án C.
Có y ' = − m 2 − 1 x − m 2 < 0 , ∀ x ∈ 1 ; 2 . Đây là hàm phân thức với tử đã mang dấu dương nên hàm số đồng biến trên 1 ; + ∞ ⇔ m 2 − 4 > 0 ⇔ m ∈ − ∞ ; − 2 ∪ 2 ; + ∞ .
Tuy nhiên hàm số phải xác định trên 1 ; + ∞ ⇒ − m ∉ 1 ; + ∞ ⇒ m ≥ − 1 ⇒ m > 2 .

Chọn C.
Phương pháp : Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải :