Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai đường thẳng song song khi và chỉ khi
![]()
Suy ra : m2+ 1- 2m = 0 hay m= 1
Chọn D.

Để hai đường thẳng song song thì:
m 2 = 2 m − 2 3 ≠ − m + 6 1 ⇔ m 2 = 2 m − 2 3 m 2 ≠ − m + 6 1 ⇔ 3 m = 4 m − 4 m ≠ − 2 m + 12 ⇔ m = 4 m ≠ 4
không tồn tại m thỏa mãn yêu cầu bài toán.
ĐÁP ÁN D

Để hai đường song song thì m=2 và m-1=1 và m<>-1
=>m=2

Đáp án: D
Để hai đường thẳng d: 2x + ( m 2 + 1)y - 3 = 0 và d': x + my - 10 = 0 song song thì:
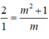
⇒ 2m = m 2 + 1 ⇔ m 2 - 2m + 1 = 0 ⇔ (m - 1 ) 2 = 0 ⇔ m = 1
Vậy với m = 1 thì d và d’ song song với nhau.

Để 2 đường thẳng đã cho trùng nhau khi và chỉ khi
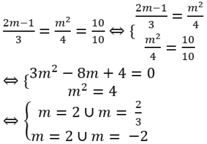
Tương đương m= 2.
Chọn C.

Lời giải:
Để hai đường thẳng trùng nhau thì trước tiên ta có: \(\frac{1}{m}=\frac{-m}{-1}=m(m\neq 0)\Leftrightarrow m=\pm 1\)
Nếu $m=1$ thì $(d_1): x-y=0$ và $(d_2): x-y=2$ không trùng nhau được
Nếu $m=-1$ thì $(d_1): x+y=0$ và $(d_2): x+y=0$ trùng nhau
Đáp án D.

Để hai đường song song thì m+3=2 và 2m-1<>4-m
=>m=-1 và 3m<>5
=>m=-1