Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Dễ thấy với m < 0 thì hàm không có tiệm
cận ngang vì x không tiến đến ∞
Với m = 0, hàm có dạng y = x + 1 và cũng
không có tiệm cận ngang
Với m > 0, ta có:
Xét lim x → + ∞ x + 1 m x 2 + 1 = lim x → + ∞ 1 + 1 x m + 1 x = 1 m
Lại có lim x → - ∞ x + 1 m x 2 + 1 = lim x → - ∞ 1 + 1 x - m + 1 x = 1 - m
⇒ Hàm có 2 tiệm cận ngang

Đáp án C
Tiệm cận ngang là đường thẳng y = 2 ⇒ 2 m = 2 ⇔ m = 1 . Khi đó y = 2 x − 3 x + 1 .

Đáp án C.
+ Tiệm cận đứng nếu có là x = − 1 m
+ Tiệm cận ngang là y = 3 m
+ Diện tích hình chữ nhật tạo thành là S = 3 m . − 1 m
⇔ 3 m 2 = 12 ⇔ m 2 = 1 4 ⇒ m = ± 1 2
(thỏa mãn)

Đáp án C
Để hàm số có 2 tiệm cận ngang khi và chỉ khi lim x → ∞ y = a ∀ a ∈ ℝ
Ta có lim x → ∞ x + 1 m x 2 + 1 = lim x → ∞ 1 + 1 x m + 1 x 2 = 1 m . Để lim x → ∞ y xác định ⇔ 1 m xác định hay m>0

Ta có ![]() đồ thị hàm số luôn có TCN y = 1
đồ thị hàm số luôn có TCN y = 1
Do đó để ycbt thỏa mãn 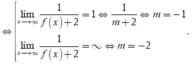
Chọn C.

Đáp án D
Đồ thị hàm số y = x + 1 x 2 − 2 mx + 2 m + 3 không có tiệm cận đứng khi và chỉ khi x 2 − 2 mx + 2 m + 3 = 0 vô nghiệm hay Δ ' = m 2 − 2 m − 3 < 0 ⇔ − 1 < m < 3 .

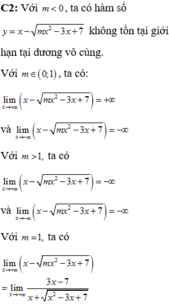





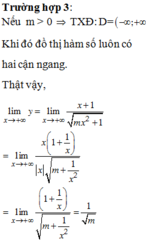
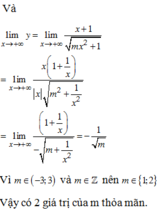
Đáp án B
Với m=1 ta có y = x + x 2 + x + 1 và lim x → + ∞ y = + ∞ lim x → − ∞ y = − 1 2
=> Đồ thị hàm số có tiệm cận ngang y = − 1 2 .
Với m = − 1 ta có y = − x + x 2 + x + 1 và lim x → + ∞ y = 1 2 lim x → − ∞ y = + ∞
=> Đồ thị hàm số có tiệm cận ngang y = 1 2 .
Với m ≠ ± 1 đồ thị hàm số không có tiệm cận ngang.