Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn phương án (D) :
Quỹ tích các điểm M nhìn đoạn thẳng AB dưới 1 góc \(120^0\) là hai cung chứa góc \(120^0\) (đối xứng nhau) dựng trên hai điểm A, B.

Chọn (D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).


Lấy đối xứng qua đường thẳng AB, ta được cung chứa góc thứ hai thỏa mãn bài toán.
Chú ý : Cung nhỏ AB trong cách dựng trên là cung chứa góc \(120^0\)

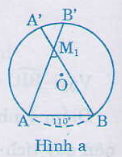
M1 là điểm bất kì nằm trong cung chứa góc 550 (hình a).
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương) Vậy góc AM1B > 550
b)
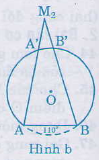
M2 là điểm bất kì nằm ngoài đường tròn (h.b), M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550
M1 là điểm bất kì nằm trong cung chứa góc 550 .
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương)
Vậy góc AM1B > 550
b)
M2 là điểm bất kì nằm ngoài đường tròn , M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550


Chọn đáp án C
Với đoạn thẳng AB và góc α ( 0 ° < α < 180 ° ) cho trước thì quỹ tích các điểm M thỏa mãn A M B ^ = α là hai cung chứa góc α dựng trên đoạn AB
Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB . Hai điểm A, B được coi là thuộc quỹ tích