K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
2
H
6 tháng 6 2023
` @Answer`
`2,(7+3x-y)(7-3x+y)`
`=(7+3x)^2 - y^2`
`3, (6/5 - 5x)^2`
`=(6/5)^2 - 2 . 6/5 . 5x+ (5x)^2`
`= 36/25 - 12x + 25x^2`
Công thức :
`(x-y)(x+y) = x^2 - y^2`
`(x+y)^2=x^2+2xy+y^2`
`+,` Đề `1:(2x+y^2)` ngoài ngoặc có gì ạ ?
KV
6 tháng 6 2023
2)
(7 + 3x - y)(7 - 3x + y)
= [7 + (3x - y)][7 - (3x + y)]
= 7² - (3x - y)²
= 49 - (3x - y)²
= 49 - (9x² - 6xy + y²)
= 49 - 9x² + 6xy - y²
DV
2
16 tháng 8 2018
(=) 1999.1999-1998.1999-1998
(=)1999.(1999-1998)-1998
(=)1999.1-1998
(=)1999-1998=1
CM
14 tháng 1 2017
Dễ thấy hai phương trình đã cho có cùng tập nghiệm, cùng số nghiệm và tương đương nhưng không có cùng điều kiện xác định.
Đáp án cần chọn là: A
BA
21 tháng 10 2019
- Bình phương của 1 tổng: (a + b)2 = a2 + 2ab + b2 = (a - b)2 + 4ab
- Bình phương của 1 hiệu: (a - b)2 = a2 - 2ab + b2 = (a + b)2 - 4ab
- Hiệu 2 bình phương: a2 - b2 = (a - b)(a + b)
- Lập phương của 1 tổng: (a + b)3 = a3 + 3a2b + 3ab2 + b3
- Lập phương của 1 hiệu: (a - b)3 = a3 - 3a2b + 3ab2 - b3
- Tổng 2 lập phương: a3 + b3 = (a + b)(a2 - ab + b2) = (a + b)3 - 3a2b - 3ab2 = (a + b)3 - 3ab(a + b)
- Hiệu 2 lập phương: a3 - b3 = (a - b)(a2 + ab + b2) = (a - b)3 + 3a2b - 3ab2 = (a - b)3 + 3ab(a - b)
DV
1
KT
21 tháng 8 2018
mik bổ sung đề, \(M=2\left(a^3+b^3\right)-3\left(a^2+b^2\right)\)
\(a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)=1-3ab\)
\(a^2+b^2=\left(a+b\right)^2-2ab=1-2ab\)
\(M=2\left(a^3+b^3\right)-3\left(a^2+b^2\right)=2\left(1-3ab\right)-3\left(1-2ab\right)\)
\(=2-6ab-3+6ab=-1\)
1 tháng 9 2019
\(4x^2-9\)
\(=\left(2x\right)^2-3^2\)
\(=\left(2x-3\right)\left(2x+3\right)\)
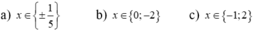
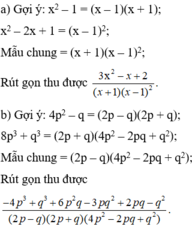
Câu b là
x2-x+1/4
Ohhh, tui hiểu r.
x2 - x + \(\dfrac{1}{4}\)
⇔ x2 - 2.\(\dfrac{1}{2}\).x + \(\left(\dfrac{1}{2}\right)^2\)
⇔ \(\left(x^2-\dfrac{1}{2}\right)^2\)