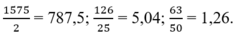Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình giải cách này hơi giống của lớp 5 nên bạn thông cảm nhé !
Gọi ba số hạng lần lượt là a, b, c, và ta giả sử \(a=\frac{3}{5}\)hay 0,6 phần, \(b=1\frac{3}{4}\)hay 1,75 phần, \(c=0,9\)phần ( Vì cả ba tỉ lệ lần lượt với \(\frac{3}{5};1\frac{3}{4};0,9\)), ta có:
\(a=130\div\left(0,6+1,75+0,9\right)\times0,6=24\)( Dạng tổng số phần của lớp 5 )
\(b=130\div\left(0,6+1,75+0,9\right)\times1,75=70\)
\(c=130\div\left(0,6+1,75+0,9\right)\times0,9=36\)
Vậy 130 viết dưới dang tổng 3 số hạng là 24, 70, 36
Mình không chắc cách làm nên bạn có thể làm cách khác nhé !

a, Tích của 2 số hữu tỉ
\(\frac{7}{20}\cdot\left(-1\right)=-\frac{7}{20}\)
b, Thương của 2 số hữu tỉ
\(1:-\frac{20}{7}=1\cdot-\frac{7}{20}=-\frac{7}{20}\)
c, Tổng của 1 số hữu tỉ dương và 1 số hữu tỉ âm
\(\frac{3}{5}+\frac{-19}{20}=\frac{12}{20}+\frac{-19}{20}=-\frac{7}{20}\)
d, Tổng của 2 số hữu tỉ âm trong đó 1 số là - 1/5
\(-\frac{1}{5}+\frac{-3}{20}=\frac{-4}{20}+\frac{-3}{20}=-\frac{7}{20}\)

cho mình sửa đề bài. viết đc dưới dạng stp hữu hạn nha


Gọi phân số tối giản phải tìm là a/b; (a; b ∈ Z; b ≠ 1), ƯCLN (a, b) = 1
Ta có a.b = 3150 = 2. 32. 52. 7 và a, b đều là ước của 3150.
Vì phân số này có thể viết được dưới dạng số thập phân hữu hạn nên b chỉ có ước nguyên tố là 2 và 5.
Do đó, b ∈ {2; 25; 50}.
- Với b = 2 thì a = 3150:2 = 1575
- Với b = 25 thì a = 3150:25 = 126
- Với b = 50 thì a = 3150:50 = 63
Vậy các phân số phải tìm là: