Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(\overrightarrow{MN=}\left(-4;-1\right)\) là vecto chỉ phương của đường thẳng cần tìm ( gọi là đường thẳng d )
Khi đó phương trình đường thẳng d có dạng : \(\left\{{}\begin{matrix}x=-4t\\y=-1-t\end{matrix}\right.\)( khi lấy điểm N là điểm đi qua)
hoặc \(\left\{{}\begin{matrix}x=4-4t\\y=-t\end{matrix}\right.\)( khi lấy điểm M là điểm đi qua)

Do d vuông góc 2x-y+4=0 nên d nhận (1;2) là 1 vtpt
Phương trình:
\(1\left(x+1\right)+2\left(y-2\right)=0\Leftrightarrow x+2y-3=0\)

\(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)
a) Đường thẳng qua A(3;2) song song với PQ nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\) làm VTCP nên có pt
\(\dfrac{x-3}{2}=\dfrac{y-2}{1}\Leftrightarrow x-2y+1=0\)
b) Đường thẳng trung trực của PQ qua trung điểm của PQ là M(2;-1) và nhận \(\overrightarrow{PQ}=(-4;-2)=2(2;1)\)làm VTPT nên có pt
\(2(x-2)+(y+1)=0\Leftrightarrow 2x+y-3=0\)

Gọi d' là đường thẳng qua M và vuông góc d
\(\Rightarrow\) Phương trình d' có dạng:
\(2\left(x-1\right)+1\left(y-4\right)=0\Leftrightarrow2x+y-6=0\)
Tọa độ H là nghiệm: \(\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\) \(\Rightarrow H\left(2;2\right)\)
Phương trình đường thẳng cần tìm:
\(1\left(x-2\right)+1\left(y-2\right)=0\Leftrightarrow x+y-4=0\)

Lấy N (1;1) và P(0;0) thuộc (d)
Gọi N' ,P' là điểm đối xứng của N,P qua M
Ta có xN' = 2*2 -1= 3
yN'= 2*1-1 =1
xP'= 2*2-0=4
yP'= 2*1-0=2
==> N'(3;1), P'(4; 2)
(d') là đường thẳng đối xứng với M qua (d) ==> (d') đi qua N' , P'
==> Phương trình (d') \(\frac{x-3}{4-3}\)= \(\frac{y-1}{2-1}\)
==> x-y-2=0
Vậy (d') là x-y-2=0
Lấy N (1;1) và P(0;0) thuộc (d)
Gọi N' ,P' là điểm đối xứng của N,P qua M
Ta có xN' = 2*2 -1= 3
yN'= 2*1-1 =1
xP'= 2*2-0=4
yP'= 2*1-0=2
==> N'(3;1), P'(4; 2)
(d') là đường thẳng đối xứng với M qua (d) ==> (d') đi qua N' , P'
==> Phương trình (d') x−34−3= y−12−1
==> x-y-2=0
Vậy (d') là x-y-2=0

a: Δ có vtcp là (2;-1) và đi qua A(1;-3)
=>VTPT là (1;2)
PTTQ là:
1(x-1)+2(y+3)=0
=>x-1+2y+6=0
=>x+2y+5=0
b: Vì d vuông góc Δ nên d: 2x-y+c=0
Tọa độ giao của d1 và d2 là:
x+2y=8 và x-2y=0
=>x=4 và y=2
Thay x=4 và y=2 vào 2x-y+c=0, ta được
c+2*4-2=0
=>c=-2
Đường thẳng MN nhận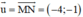 là 1 vtcp
là 1 vtcp
⇒ MN nhận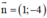 là 1 vtpt
là 1 vtpt
Mà M(4; 0) thuộc đường thẳng MN
⇒ Phương trình đường thẳng MN: 1(x - 4) – 4(y - 0) = 0 hay x – 4y – 4 = 0.