Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\)(E)
Thay x=0 và y=-4 vào (E), ta được:
16/b^2=1
=>b=4
F2(3;0)
=>c=3
=>căn a^2-16=3
=>a^2-16=9
=>a=5
=>x^2/25+y^2/16=1
F1(-2;0) nên c=-2
=>c^2=4
=>c^2=a^2-b^2=4
=>a^2=b^2+4
(E): x^2/a^2+y^2/b^2=1
Thay x=2 và y=3 vào (E), ta được:
2^2/a^2+3^2/b^2=1
=>4/a^2+9/b^2=1
=>\(\dfrac{4}{b^2+4}+\dfrac{9}{b^2}=1\)
=>\(\dfrac{13b^2+36}{b^2\left(b^2+4\right)}=1\)
=>b^4+4b^2-13b^2-36=0
=>b^2=12
=>b=2căn 3
=>a=4
=>(E): x^2/16+y^2/12=1
Phương trình chính tắc của elip có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\).
Elip đi qua \(A\left( {5;0} \right)\) nên ta có \(\frac{{{5^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Leftrightarrow {a^2} = 25\)
Mặt khác elip có một tiêu điểm \({F_2} = \left( {3;0} \right)\) nên ta có \(c = 3\), suy ra \({b^2} = {a^2} - {c^2} = 25 - {3^2} = 16\)
Vậy phương trình của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\).
F2(5;0)
=>c=5
(E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
9/b^2=1
=>b=3
c^2=a^2-b^2
=>a^2=5^2+3^2=34
=>(E): x^2/34+y^2/9=1
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
Gọi Elip cần tìm có dạng : (E) :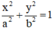 
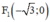là tiêu điểm của (E) ⇒ a2 – b2 = 3 ⇒ a2 = b2 + 3
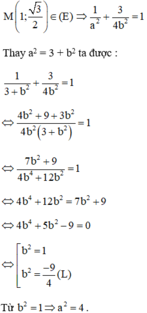
Phương trình chính tắc của Elip là :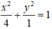 
\(F_1F_2=2c=2\sqrt{5}\)
\(\Rightarrow c=\dfrac{2\sqrt{5}}{2}=\sqrt{5}\)
\(\left(E\right)\) qua \(\left(5;0\right)\Rightarrow a=5\)
Ta có : \(b=\sqrt{a^2-c^2}\)
\(\Rightarrow b^2=a^2-c^2\)
\(\Rightarrow b^2=5^2-\sqrt{5}^2\)
\(\Rightarrow b^2=25-5=20\)
Vậy \(PTCT\left(E\right):\dfrac{x^2}{25}+\dfrac{y^2}{20}=1\)
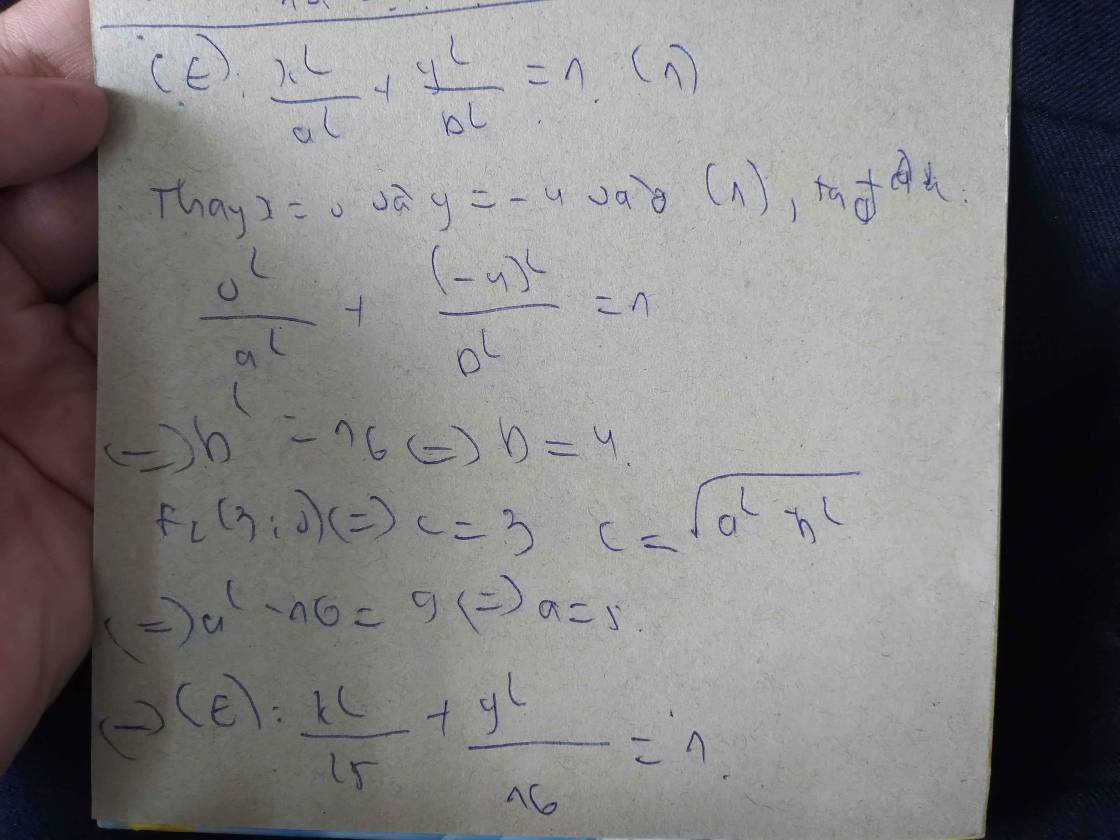
F1(\(-\sqrt{3};0\)) => c=\(\sqrt{3}\)
có: \(b^2=a^2-c^2=a^2-3\)
pt elip di qua M:
\(\dfrac{3}{a^2}+\dfrac{1}{4b^2}=1\)
\(\Leftrightarrow\dfrac{3}{a^2}+\dfrac{1}{4a^2-12}=1\)
dat a^2=t (t>0)
\(\Leftrightarrow\dfrac{3}{t}+\dfrac{1}{4t-12}=1\\ \Leftrightarrow12t-36+t=4t^2-12t\)
\(\Leftrightarrow4t^2-25t+36=0\\ \Leftrightarrow\left[{}\begin{matrix}t=4\\t=\dfrac{9}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a^2=4\\a^2=\dfrac{9}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}b^2=1\\b^2=-\dfrac{3}{4}\left(loai\right)\end{matrix}\right.\)
=>ptelip: \(\dfrac{x^2}{4}+\dfrac{y^2}{1}=1\)