Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Viết các biểu thức sau dưới dạng lũy thửa của một số hữu tỉ:
\(\frac{\left(5^4-5^3\right)^3}{125^4}\)

\(\frac{\left(5^4-5^3\right)^3}{125^4}\)
\(=\frac{500^3}{125^4}\)
\(=\frac{\left(125.4\right)^3}{125^4}\)
\(=\frac{4^3}{125}=\frac{4^3}{5^3}=\left(\frac{4}{5}\right)^3\)

a) \(8^{15}.4^{13}=\left(2^3\right)^{15}.\left(2^2\right)^{13}=2^{45}.2^{26}=2^{71}\)
b) \(\left(\frac{1}{2}\right)^{18}.\left(\frac{1}{4}\right)^{28}=\left(\frac{1}{2}\right)^{18}.\left(\frac{1}{2^2}\right)^{28}=\frac{1}{2^{18}}.\frac{1}{2^{56}}=\frac{1}{2^{74}}=\left(\frac{1}{2}\right)^{74}\)
c) \(9^{12}.27^{10}=\left(3^2\right)^{12}.\left(3^3\right)^{10}=3^{24}.3^{30}=3^{54}\)
a) = (23)15. (22)13 = 245.226 = 271
b) = \(\left(\frac{1}{2}\right)^{18}.\left(\left(\frac{1}{2}\right)^2\right)^{28}=\left(\frac{1}{2}\right)^{18}.\left(\frac{1}{2}\right)^{56}=\left(\frac{1}{2}\right)^{18+56}=\left(\frac{1}{2}\right)^{74}\)
c) = (32)12.(33)10 = 324.330 = 324+30 = 354

Trả lời:
a, \(15^8.9^4\)
\(=15^8.\left(3^2\right)^4\)
\(=15^8.3^8\)
\(=45^8\)
b, \(27^2:25^3\)
\(=\left(3^3\right)^2:\left(5^2\right)^3\)
\(=3^6:5^6\)
\(=\left(\frac{3}{5}\right)^6\)
Hok Tốt!!!!
a. 158 . 94
= 158 . (32)4
= 158.38
= (15.3)8
= 458
b. 272 : 253
= (33)2 : (52)3
= 36 : 56
= \(\left(\frac{3}{5}\right)^6\)

\(\frac{8^{11}.3^{17}}{27^{10}.9^{15}}=\frac{8^{11}.3^{17}}{3^{30}.3^{30}}=\frac{8^{11}}{3^{13}.3^{30}}=\frac{8^{11}}{3^{43}}\)
\(\frac{\left(5^4-5^3\right)^3}{125^4}=\frac{[\left(5-1\right).5^3]^3}{5^{12}}=\frac{\left(4.5^3\right)^3}{5^{12}}=\frac{64.5^9}{5^{12}}=\frac{64}{5^3}=\left(\frac{4}{5}\right)^3\)
\(\frac{4^{20}-2^{20}+6^{20}}{6^{20}-3^{20}+9^{20}}=\frac{2^{40}-2^{20}+6^{20}}{6^{20}-3^{20}+3^{40}}=\frac{2^{20}.\left(2^{20}-1+3^{30}\right)}{3^{20}.\left(2^{20}-2+3^{20}\right)}=\frac{2^{20}}{3^{20}}=\left(\frac{2}{3}\right)^{20}\)

a: \(\left(\dfrac{1}{5}\right)\cdot\left(\dfrac{1}{5}\right)^{15}=\left(\dfrac{1}{5}\right)^{1+15}=\left(\dfrac{1}{5}\right)^{16}\)
b: \(\left(-10,2\right)^{10}:\left(-10,2\right)^3=\left(-10,2\right)^{10-3}=\left(-10,2\right)^7\)
c: \(\left[\left(-\dfrac{7}{9}\right)^7\right]^8=\left(-\dfrac{7}{9}\right)^{7\cdot8}=\left(-\dfrac{7}{9}\right)^{56}\)

a) \(\frac{6}{5}.{\left( {1,2} \right)^8} = 1,2.{(1,2)^8} = {(1,2)^{1 + 8}} = {(1,2)^9}\)
b) \({\left( {\frac{{ - 4}}{9}} \right)^7}:\frac{{16}}{{81}} = {\left( {\frac{{ - 4}}{9}} \right)^7}:{\left( {\frac{{ - 4}}{9}} \right)^2} = {\left( {\frac{{ - 4}}{9}} \right)^{7 - 2}} = {\left( {\frac{{ - 4}}{9}} \right)^5}\)

c) \(\left(\dfrac{5}{4}\right)^4:\left(\dfrac{15}{2}\right)^4=\left(\dfrac{5}{4}:\dfrac{15}{2}\right)^4=\left(\dfrac{1}{6}\right)^4\)
d) \(10^4:16=10^4:2^4=\left(10:2\right)^4=5^4\)
e) \(\left(-2\right)^3.125=\left(-2\right)^3.5^3=\left(-2.5\right)^3=-10^3\)
f) \(64^3:\left(-2\right)^9=64^3:\left(-8\right)^3=\left(64:-8\right)^3=-8^3\)

a) \(15^8\cdot2^4\)
\(=\left(15^2\right)^4\cdot2^4\)
\(=225^4\cdot2^4\)
\(=\left(225\cdot2\right)^4\)
\(=450^4\)
b) \(27^5:32^3\)
\(=\left(3^3\right)^5:\left(2^5\right)^3\)
\(=3^{15}:2^{15}\)
\(=\left(\dfrac{3}{2}\right)^{15}\)
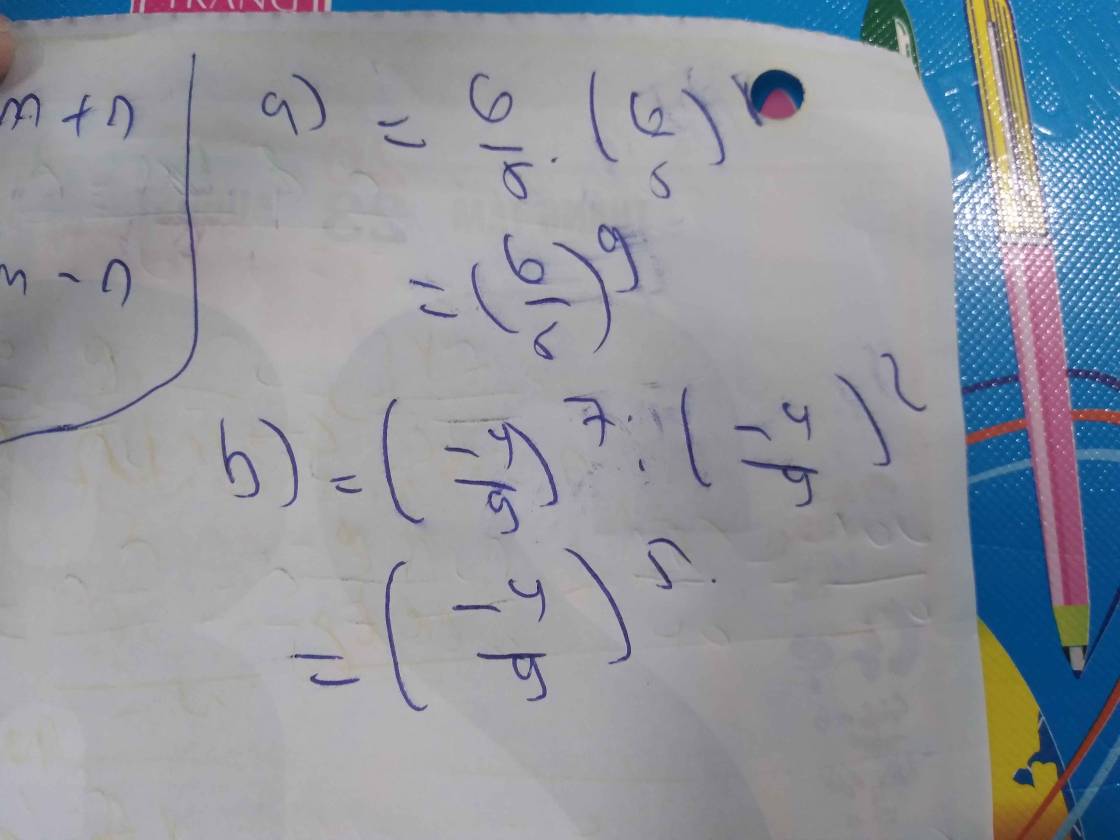
nhanh nha các bn
Ta có :
a) \(\frac{21^{30}}{63^{15}}=\frac{\left(21^2\right)^{15}}{63^{15}}=\left(\frac{21^2}{63}\right)^{15}\)
b) \(\frac{28^9.30^9}{105^9}=\frac{\left(28.30\right)^9}{105^9}=\frac{840^9}{105^9}=\left(\frac{840}{105}\right)^9=8^9\)