K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
13 tháng 10 2016
\(\frac{3x-1}{40x-5}=\frac{25-3x}{5x-34}\)
\(\Leftrightarrow\left(3x-1\right).\left(5x-34\right)=\left(40x-5\right).\left(25-3x\right)\)
\(\Leftrightarrow15x^2-102x-5x+34=1000x-120x^2-125-15x\)
\(\Leftrightarrow15x^2-107x+34=985x-120x^2-125\)
Làm tiếp nha không bk đúng kh nữa
28 tháng 10 2021
Do trong hình có 2 đường thẳng cùng vuông góc với một đường thẳng nên 2 đt đó // với nhau
Do đó \(x+115^0=180^0\) (2 góc ở vị trí trong cùng phía)
Vậy \(x=180^0-115^0=65^0\)
TA
1
XO
1 tháng 9 2019
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau ta có :}\)
\(\Rightarrow\frac{40x-20y}{5}=\frac{10z-40x}{7}=\frac{20y-10z}{9}=\frac{40x-20y+10z-40x+20y-10z}{5+7+9}=0\)
\(\Rightarrow40x=20y\left(1\right);\)
\(20y=10z\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow40x=20y=10z\)
\(\Rightarrow\hept{\begin{cases}40x=20y\\20y=10z\end{cases}\Rightarrow\hept{\begin{cases}\frac{x}{20}=\frac{y}{40}\\\frac{y}{10}=\frac{z}{20}\end{cases}\Rightarrow}\hept{\begin{cases}\frac{x}{20}=\frac{y}{40}\\\frac{y}{40}=\frac{z}{80}\end{cases}}\Rightarrow\frac{x}{20}=\frac{y}{40}=\frac{z}{80}\Rightarrow\frac{2x}{40}=\frac{3y}{120}=\frac{4z}{320}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{20}=\frac{y}{40}=\frac{z}{80}=\frac{2x}{40}=\frac{3y}{120}=\frac{4z}{320}=\frac{2x+3y+4z}{40+120+320}=\frac{48}{480}=\frac{1}{10}\)
\(\Rightarrow10x=20\Rightarrow x=2;\)
\(10y=40\Rightarrow y=4;\)
\(10z=80\Rightarrow z=8\)
Vậy x = 2 ; y = 4 ; z = 8
PT
1
CM
18 tháng 7 2018
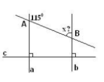
Kí hiệu như hình vẽ ta có:
a ⊥ c, b ⊥ c nên suy ra a // b
Do đó x + 115o = 180o (hai góc trong cùng phía)
Nên x = 180o - 115o = 65o
2 tháng 9 2019
Từ giả thiết \(\Rightarrow\frac{2.\left(40x-20y\right)}{5}=\frac{2.\left(10z-40x\right)}{7}=\frac{2.\left(2y-10z\right)}{9}\)
\(\Leftrightarrow\frac{80x-40y}{5}=\frac{20z-80x}{7}=\frac{40y-20z}{9}\)
26 tháng 7 2023
a: góc mOd=180-50=130 độ
b: góc mOc<góc mOd
=>OC nằm giữa Om và Od
=>góc mOc+góc cOd=góc mOd
=>góc cOd=90 độ
c: góc dOc là góc vuông
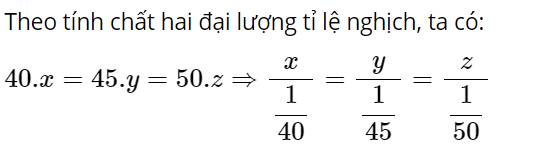
\(40x=\dfrac{x}{\dfrac{1}{40}} \)
Ta có
\(\dfrac{x}{\dfrac{1}{40}}=x:\dfrac{1}{40}=x\times\dfrac{40}{1}=40x\)