Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
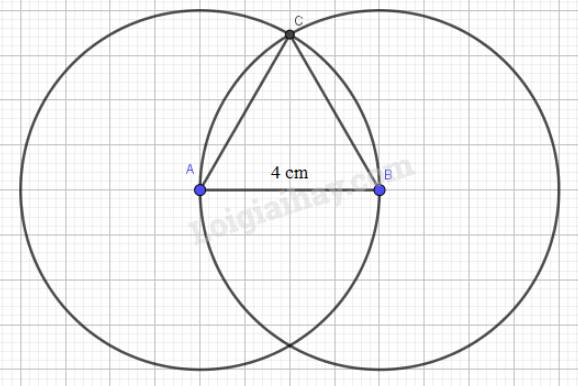
- Sử dụng thước vẽ đoạn thẳng AB bằng 4 cm.
- Lấy A, B làm tâm, vẽ hai đường tròn bán kính 4 cm.
Gọi C là một trong hai giao điểm của hai đường tròn. Nối C với A và C với B ta được tam giác đều ABC.

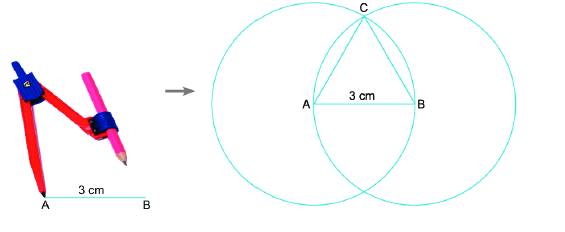
Vì C thuộc đường tròn tâm A bán kính 3 cm nên AC=3 cm.
Vì C thuộc đường tròn tâm B bán kính 3 cm nên BC=3 cm.
Vậy ba cạnh của tam giác bằng nhau.
Ba góc của tam giác bằng nhau và bằng \(60^0\).

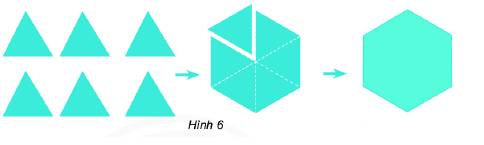
a) Ghép 6 tam giác đều thành hình mới.
b) Hình vừa nhận được có các góc bằng nhau, các cạnh bằng nhau.
Đây là hình lục giác đều.

- Gọi tam giác đều ABC, đường cao AH .
- Áp dụng định lý pitago vào tam giác AHB vuông tại H.
\(AH=\sqrt{AB^2-BH^2}\approx3,9\)
- Từ trung điểm của BC lấy H kẻ đường thẳng vuông góc từ H với BC được điểm A sao cho AH = ~ 3,9 cm .

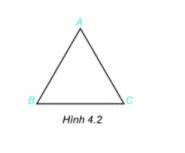
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
vẽ ra nha mn :<<<