K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CB
13 tháng 2 2017
Cách vẽ: 
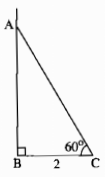
– Vẽ đoạn AC=2cm,
– Trên cùng một nửa mặt phẳng bờ AC vẽ tia Ax và Cy sao cho góc ∠CAx = 900, ∠ACy = 600
CB
13 tháng 2 2017
Cách vẽ:
– Vẽ đoạn AC=2cm,
– Trên cùng một nửa mặt phẳng bờ AC vẽ tia Ax và Cy sao cho góc ∠CAx = 900, ∠ACy = 600
PD
0
SG
1
9 tháng 2 2022
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
Suy ra: BA=BE; DA=DE
=>BD là đường trung trực của AE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDCF cân tại D
MF
2
DA
8 tháng 1 2019
cạnh ab là: (9=7):2= 8 cm
cạnh ac là: 9-8= 1 cm
â= 90? /mk ko hỉu/
k mk nhé
8 tháng 1 2019
Ta có:\(\Delta ABC,\widehat{A}=90^o\Rightarrow\Delta ABC\) vuông tại A.
Theo bài ra ta có:
\(AB+AC=9cm\) (1)
\(AB-AC=7cm\) (2)
Xét tổng (1) và (2):
\(AB+AC+AB-AC=9cm+7cm\)
\(2.AB=16cm\)
\(AB=16cm:2\)
\(AB=8cm\)
Thay AB=8cm vào (1),ta được:
AB+AC=9cm
\(\Leftrightarrow8cm+AC=9cm\)
\(\Leftrightarrow AC=1cm\)
Ta có định lý Py-ta-go về tam giác cân:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+1^2\)
\(\Leftrightarrow BC^2=65\)
\(\Leftrightarrow BC=\sqrt{65}\)
\(BC\approx8cm\)
Vậy BC\(\approx\)8 cm.
Hình như đề bài có gì đó sai sai nên theo mình thì chỉ ước lượng BC=8cm.Chứ thật ra thì BC là số thập phân vô hạn tuần hoàn cơ.
Cái đó thì tự đi mà làm chứ bạn
Nếu người khác vẽ cho bạn thì làm sao bn vẽ ra vở chính xác được
Bạn tự làm đi, đơn giản mà.