



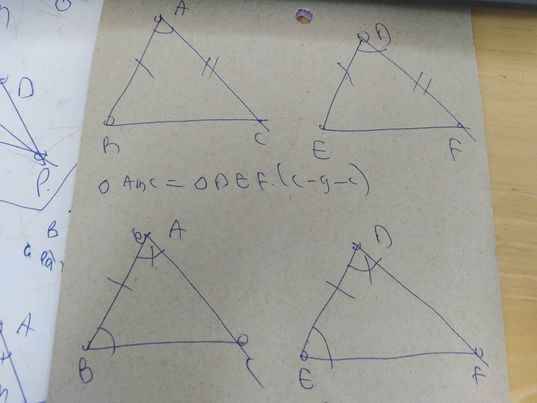
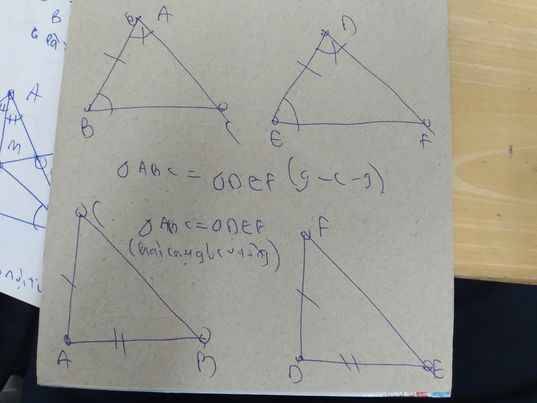
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




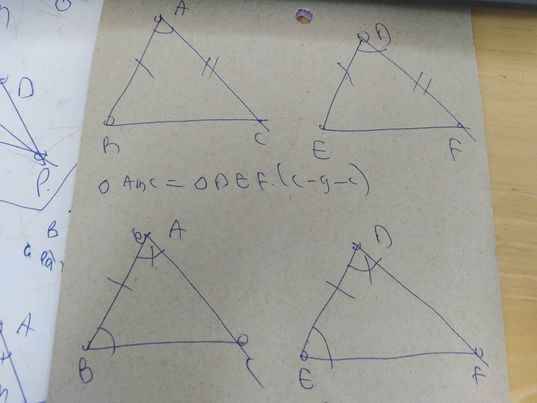
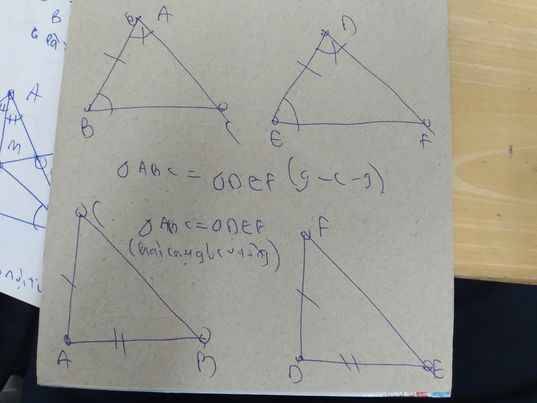



1/ Hai góc đối đỉnh thì bằng nhau
2/ Trong tam giác thường: cạnh-canh-cạnh ; cạnh-góc-cạnh; góc-cạnh-góc
Trong tam giác vuông : cạnh huyền- góc nhọn; cạnh huyền-cạnh góc vuộng
A B C M
3/ Xét \(\Delta ABM\) và \(\Delta ACM\) có:
BM= CM ( AM là đường trung trực)
Góc AMB = góc AMC = 90o
AM chung
-> \(\Delta ABM\)= \(\Delta ACM\) (c.g.c)
-> AB=AC(cạnh tương ứng)
-> Tam giác ABC cân tại A
3/

Các tính chất ở cá câu a ,b được suy ra từ định lí "Tổng ba góc của một tam giác bằng 180o".
Tính chất ở câu c được suy ra từ định lí "Trong một tam giác cân hai góc ở đáy bằng nhau".
Tính chất ở câu d được suy ra từ định lí: Nếu một tam giác có ba góc bằng nhau thì tam giác đo là tam giác cân.
Các tính chất ở các câu (a); (b) được suy ra từ định lí: “Tổng ba góc của một tam giác bằng nhau bằng 1800”.
Tính chất ở câu (c) được suy ra từ định lí: “Trong tam giác cân, hai góc ở đáy bằng nhau”.
Tính chất ở câu (d) được suy ra từ định lí: “Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân”.

Bài 1:
I. Trường hợp bằng nhau thứ nhất của tam giác cạnh – cạnh – cạnh:
1) Vẽ tam giác biết độ dài 3 cạnh: (HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = 3cm, BC = 5cm, AC = 4cm.
2) Trường hợp bằng nhau cạnh – cạnh – cạnh:
“Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.”
II. Trường hợp bằng nhau thứ nhất của tam giác cạnh – góc – cạnh:
1) Vẽ tam giác biết độ dài 2 cạnh và 1 góc xen giữa:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AB = BC = 4cm,
2) Trường hợp bằng nhau cạnh – góc – cạnh:
“Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.”
* Lưu ý: Cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau thì mới kết luận được hai tam giác bằng nhau.
III. Trường hợp bằng nhau thứ nhất của tam giác góc – cạnh – góc:
1) Vẽ tam giác biết độ dài 1 cạnh và 2 góc kề:
(HS tự nêu các bước vẽ)
VD: Vẽ rABC biết AC = 5cm,
2) Trường hợp bằng nhau góc – cạnh – góc:
“Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.”
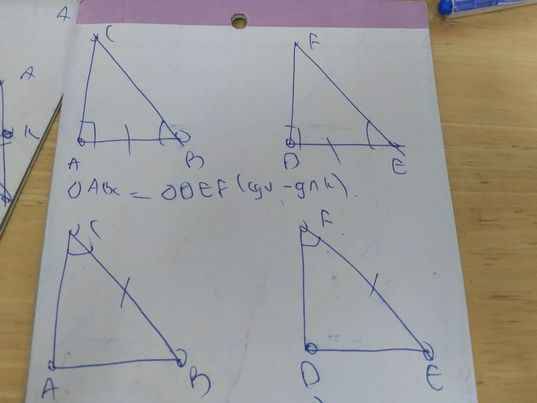
* Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
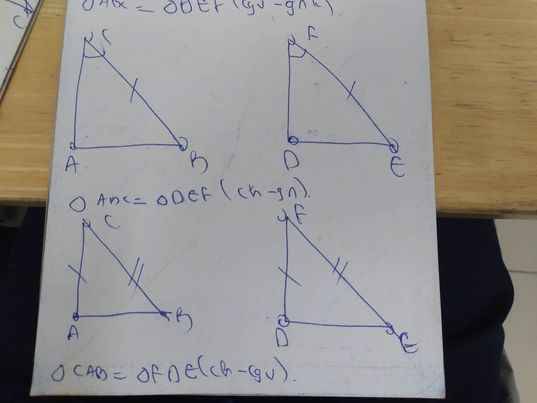
* Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề ấy cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g-c-g)
* Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (ch-gn)